BACKGROUND

There are an estimated 3.6 million wheelchair users in the United States (Brault, 2012). Of these, 15% could be expected to use electric powered wheelchairs (EPW) (Cooper, Cooper, & Boninger, 2008). With the aging of the US population, these numbers are expected to grow. EPWs provide community integration, independence, and increased quality of life for persons with disabilities (Edwards & Mccluskey, 2010). Still, EPW users confront challenges when going outdoors including slopes, steps, uneven surfaces, and other environmental barriers (Ding & Cooper, 2005; Ståhle, Brandt, & Iwarsson, 2004). In the US, EPWs are typically purchased by Medicare, Medicaid, private insurance, the Veterans Administration, or State offices of vocational rehabilitation (Buning, Schmeler, & Crane, 2006). Payment guidelines often restrict justification for device functionality to that which is needed in the home. A result of this restriction is that typical EPWs give poor performance on inclines and cross slopes, do not provide sufficient traction on slippery surfaces, and are incapable of surmounting obstacles higher than 3 inches – e.g. curbs (Daveler et al., 2015). EPW users may adapt their driving behavior in order to avoid such obstacles (Daveler et al., 2015; Ståhle et al., 2004), but such compromises may prevent people from visiting the places they might otherwise choose to go.

Besides limiting independence, environmental barriers can lead to injuries for EPW users. Data from 2003 found that there were over 100,000 emergency room visits resulting from wheelchair accidents – 65% of which could be attributed to tips and falls (Xiang, Chany, & Smith, 2006). A survey to characterize wheelchair incidents found that 42% could be considered as tips and falls, and that hospitalizations were weighted toward those categories (Gaal, Rebholtz, Hotchkiss, & Pfaelzer, 1997). The same survey found that 79% of tips and falls occurred on rough ground or non-level surfaces. A study to categorize wheelchair incidents found that, of 95 respondents, 55% had experienced at least one incident in the previous three years, and 88% of those incidents were tips and falls (Chen et al., 2011).

In order to promote safety and independence for EPW users when they travel outside the home, the Mobility Enhancement Robotic Wheelchair (MEBot) was developed. Its specific functions of self-leveling when traversing inclines and cross slopes, curb climbing, and traction control were chosen based on input from focus groups conducted with EPW users, who identified ramps, curbs, and uneven and soft surfaces as their greatest obstacles (Daveler et al., 2015).

Daveler et al described the mechanical design of the MEBot (Daveler et al., 2015). The features relevant to self-leveling include: each of the two (2) drive wheels and two (2) rear casters being mounted on pivoting linkages moved by double acting pneumatic actuators that permit them to be independently raised and lowered, an inertial measurement unit (IMU), incorporating an accelerometer and gyroscope that measure orientation, and position sensors that measure the stroke extension of each pneumatic cylinder.

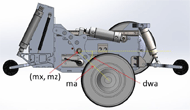
In a previous version of the MEBot, the self-leveling algorithm multiplied a rotation matrix with pitch and roll angles by a matrix containing the initial wheel positions in order to determine the new desired wheel positions to keep the frame level (Candiotti et al., 2016). A redesign of the pneumatic system and wheel linkages to increase the maximum vertical wheel travel required a more complete consideration of the linkage motion’s geometry.

GEOMETRIC MODEL

In order to know the wheel position from the displacement of the pneumatic actuator, a geometric model of each wheel’s mechanical system was created. For both the driving wheels and the rear casters, movement of the pneumatic actuator can be seen to vary the angle of the arm on which each wheel is mounted relative to a reference line on the wheelchair frame.

The angle between the drive wheel arm and a line extending horizontally from the point around which the arm pivots, dwa, can be calculated from the displacement of the  actuator through a series of trigonometric relations. The position at which the drive wheel contacts the ground (dwx, dwz), relative to the main pivot point (mx, mz), with ma being the length of the drive wheel arm, is given simply by

$$(\mathrm{dwx},\mathrm{dwz})=(\mathrm{mx}+\mathrm{ma}\ast \cos \mathrm{dwa},\mathrm{mz}-\mathrm{ma}\ast \sin \mathrm{dwa})$$

 

The position of the rear caster can be related to the stroke of its actuator by similar means.

algorithm description

Determining Pneumatic Positions

When self-leveling is initialized, all four actuators – front left, front right, rear left, and rear right – are set to the midpoint of the wheelchair’s ground clearance. As the minimum and maximum ground clearances are not the same for the drive wheels and rear casters, the midpoint is calculated from the greater of the minima and the lesser of the maxima. This ground clearance is defined as 0 on the z-axis for the self-leveling algorithm.

The positions of the wheels in the x-axis can be calculated, and the 0 is defined as the midpoint between the drive wheels and the rear casters at this middle ground clearance. The positions of the wheels in the y-axis do not change with pneumatic position, and the zero position along this axis corresponds to the midline of the wheelchair.

A matrix, currentM, gives the coordinates of each wheel in the, above described, coordinate system. For compatibility with the transformation matrix, the currentM matrix must be expanded to 4 x 4, with the last row being occupied by ones

A transformation matrix takes inputs for pitch φ (phi), and roll θ (theta), measured from the IMU sensor, to perform a rotation on the current wheel positions. The transformation matrix also performs a translation to refer the new wheel positions to the bottom of the frame – a subtraction of the midpoint ground clearance midz.

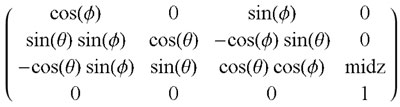
The product of the rotation matrix and currentM gives the desired wheel positions to maintain the frame level. The Z-values, the vertical position of each wheel relative to the bottom of the frame, are then fed into linearized equations to obtain the corresponding displacement of each actuator. These positions are then propagated to the lower level control system to move the pneumatic actuators.

Calculating Current Wheel Positions

Based on the current position of each actuator, and the geometric model, the actual position of each wheel can be calculated in the X, Y, and Z axes. The pitch and roll angles of the plane determined by any three wheels of the MEBot can be calculated by taking the cross product of the vectors from any one of those wheels to the other two – e.g. the cross product of the vector from the rear left caster to the front right drive wheel with the vector from the rear left caster to the front left drive wheel.

The current positions from the geometric model are also used to update the wheel position matrix, currentM. However, the midpoint ground clearance must be added to each wheels’ Z-values to translate them back into the original coordinate system.

When the wheelchair seat reaches the desired position, the IMU sensor will read zero in both the pitch and roll directions. Any deviation from levelness – whether due to error in the linearization of the model, error introduced by the transformation matrix not accounting for the movement of the wheels in the X-direction, or a change in the slope encountered by the wheelchair – will cause the IMU sensor to register a nonzero value. If this value is greater than the threshold the self-leveling algorithm will iterate until both pitch and roll are below their respective thresholds. Because the wheel position matrix, currentM, includes the changes in the X-position of the wheels resulting from the geometry of the mechanical linkage, these X-direction changes – not otherwise accounted for – will not affect self-leveling performance over slowly changing angles.

Simulation results

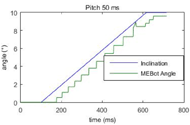
The preceding algorithm was implemented in MATLAB (The MathWorks, Natick, MA), and simulations were run in order to test its effectiveness. For each simulation, an example terrain was translated into time varying pitch and roll values relative to the horizontal. Since the pitch and roll angles measured by the IMU sensor are measured for the frame relative to the horizontal plane, they are equivalent to the actual angle of the terrain minus the current angle of the wheelchair. The simulation also allows for introduction of a delay between measurement of the angle and response of the self-leveling system.

If climbing a continuous 10° slope, without self-leveling, the angle of inclination of the wheelchair would increase linearly from 0° to 10°, as first the drive wheels, then the entire wheelbase transitions onto the slope, then remain at 10° thereafter. Given the MEBot’s 28.2 inches (71.63 cm) wheelbase length at its middle ground clearance, traveling at a reasonable walking speed of approximately 3.11 mph (5 km/h), and neglecting the change in wheelbase length that occurs during self-leveling, the MEBot will transition entirely on to the 10° slope in approximately 0.516 seconds. Therefore, a profile was constructed representing the MEBot approaching the slope for 100 ms – no change in angle – transitioning onto the slope for 516 ms – linear increase in actual angle – and continuing to climb the 10° slope thereafter – constant 10° angle. The simulation was run with an angle threshold of +/-0.5° – chosen to balance rejection of noise from the IMU, constant adjustment of the pneumatics, and comfort of the user – and a delay of 50 ms – representing the time between detection of the angle by the IMU sensor and response of the self-leveling system.

The stair steps evident in the graph result from the algorithm not reacting until the angle measured by the IMU exceeds the 0.5° threshold. The simulation shows a maximum deviation of 1.47° between the actual angle and the corrected angle – this deviation being the angle experienced by a seated user. The deviation results from a combination of the 0.5° threshold and the delay in the system’s response while the MEBot continues to climb the slope. A change in the stairstep movement can also be seen at 564 ms into the simulation – 464 ms after the MEBot reaches the incline.

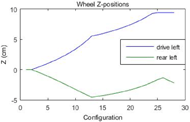
In order to investigate this behavior, the resulting wheel positions from each stepwise change in configuration were graphed for both the drive wheels and the rear casters. As for this simulation the motion of left and right wheels will be the same, only one side is shown.

As shown in figure 3, the positions of the drive and rear wheels diverge from the midpoint until the 13th iteration of the self-leveling algorithm – at which point the displacement of the rear casters changes direction. At the 25th new wheel configuration, the drive wheels run out of travel, and the rear casters again reversed direction. Changing the algorithm to account for movement of the center of the wheelbase with changes of wheel position did not eliminate this behavior.

The same slope climbing simulation was modified in order to allow the introduction of noise into the pneumatic system. After each new calculation of desired pneumatic stroke position, a random value between +0.2 inches and -0.2 inches (+/-0.5 cm) was added to each value. Along with the introduction of oscillations, the resulting error from levelness can be seen to have increased from 1.47° to 3.74°.

DISCUSSION

Simulations show the self-leveling algorithm presented here is capable of maintaining the wheelchair frame level over gradual changes in angle in both pitch and roll. Delays in reaction of the system will, however, result in the angle of incline experienced by the user being greater than the specified threshold values. Further, errors in the positions of the pneumatic actuators can introduce oscillations in the attitude of the frame. The simulation also showed the rear caster ground clearance reversing direction.

Future work will include further examination of the relationship between the algorithm and the geometric model to determine the reason for change in rear caster direction. As the pneumatic actuators are mechanical systems, errors in their displacements must be expected. A wider threshold could reduce oscillations, but may also result in greater oscillations when the threshold is exceeded. The algorithm has also been implemented on the physical prototype, and is currently being validated through real-world testing.

CONCLUSIONS

The present paper has introduced an algorithm to control a wheelchair capable of self-leveling that considers the specific geometry of its motion. Simulations demonstrate that the algorithm is effective when sources of mechanical noise are low, but that errors in movement of the mechanical system can cause oscillations that may be undesirable for users. Nonetheless, the algorithm provides a foundation for further refinement informed by additional simulations and real-world testing.