Mechanical Efficiency of the Push during Uphill Wheelchair Propulsion: Implications toward Adaptation and Method Validity
ABSTRACT
Analyzing the mechanical efficiency of the push, or the Contribution of the Tangential Force (CTF) to the total applied force, provides insight into the nature of wheelchair propulsion. Previous research has found CTF to be low for simulated level propulsion. It was hypothesized that CTF would be affected by uphill propulsion. The study involved 17 wheelchair users propelling on four treadmill grades, ranging from 2% to 8% while the applied handrim force and moment were measured. CTF was found to increase with increasing grade. However, increases in CTF exceeded 1.0, the physical limit of the measure. Values of CTF beyond 1.0 were determined to be the result of users adapting to uphill propulsion by applying an appreciable hand moment. The traditional method of calculating CTF, which assumes a negligible hand moment, does not appear to be valid for uphill propulsion.
Keywords :
wheelchair, propulsion, biomechanics, handrim, efficiency, CTF
BACKGROUND
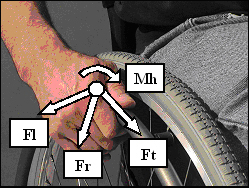
Analyzing the forces applied to the handrim during wheelchair propulsion offers the opportunity to gain insight into the mechanics of the process. One of the areas of interest when analyzing the force applied to the handrim is its mechanical efficiency, or how well it is aligned with the handrim. The only component (direction) of force that causes the wheel to rotate is that which follows the path of the handrim, referred to as the tangential component (Ft) (Figure 1). The other components of force are in the radial (Fr) and lateral (Fl) directions. The radial direction is downward into the handrim and the lateral direction is outward to the side (Figure 1). The radial and lateral components of force do not cause the wheel to rotate and would appear to be wasted energy. However, the role of these force components is still unclear. They may be an important aspect of propulsion by ensuring a secure grip on the handrim.
 |
|---|
The mechanical efficiency of the force is generally expressed as a ratio of the tangential force component to the resultant, or total force magnitude. It is also expressed more rigorously as the same ratio but squared. The mechanical efficiency ratio is known by several names including the Mechanical Effective Force (MEF), Fraction of Effective Force (FEF), and the Contribution of Tangential Force (CTF). CTF will be used to describe mechanical efficiency of the force in this study. CTF has been found to be low, ranging from 0.26 [1] to 0.56 [2] for propulsion on a wheelchair ergometer. By providing feedback to the user during ergometer propulsion, CTF has been improved. However, the increases in CTF resulted in decreased metabolic efficiency, suggesting that the non-tangential force components may be necessary for efficient propulsion [3].
RESEARCH QUESTION
The research analyzing mechanical efficiency of the force during propulsion has been done while pushing on a stationary wheelchair ergometer, on simulated level surfaces. Pushing uphill differs from pushing on level surfaces in that it: 1) is generally slower, 2) requires larger forces, and 3) generally requires the user to lean more forward to maintain stability. This study investigated the hypothesis that users increase their applied hand moment in response to pushing uphill and that the resulting CTF values determined using the traditional method exceed the physical limit of the measure.
METHODS
Full-time manual wheelchair users with at least one year of experience were recruited to participate in the study. The subjects' rear wheels were replaced with instrumented test wheels. The right test wheel was equipped with a commercially available 6DOF load cell (ATI, Garner, NC) to measure the force and moment applied to the handrim. Signals were sampled at 480 Hz (National Instruments, Austin, TX).
Subjects were asked to propel their wheelchair on a treadmill for four one-minute periods at prescribed speeds at different treadmill grade conditions. Prescribed propulsion speeds were chosen to be comfortable for a wide range of wheelchair users. The four grade and speed combinations tested included: 1) 2% grade at 0.94 m/s (2.1 mph), 2) 4% grade at 0.53 m/s (1.2 mph), 3) 6% grade at 0.36 m/s (0.8 mph), and 4) 8% grade at 0.27 m/s (0.6 mph). The first 30 seconds of each propulsion bout was used as an acclimation period. Handrim loads were recorded during the second half of each propulsion bout. The experimental setups for the 2% and 8% grade conditions are shown in Figure 2.
 |
|---|
The first 15 pushes from each data file were used in the analysis. For each
push analyzed, CTF values were determined for each handrim force sample and
then averaged across the push. CTF values were determined using the following
relationship: 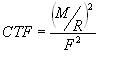
where M is the measured moment about the wheel axle, R is the outside radius of the handrim, and F is the resultant force applied by the user's hand. This relationship has been used in previous research and is based on the assumption that there is a negligible moment applied by the hand. The total moment applied to the handrim, M is a combination of both a hand moment (Mh) (Figure 1) along with the product of Ft and R. The validity of this relationship has not been established for uphill propulsion. Resulting CTF values for each grade condition were compared using an ANOVA for repeated measures with grade condition as the main factor. A post-hoc Tukey test with significance set to p<0.05 was used to determine differences between grade conditions.
RESULTS
Seventeen manual wheelchair users gave written consent and participated in the study. Seven of the subjects were female. The average age of the subjects was 37 years old (sd=12) and the average wheelchair experience was 14 years (sd=10).
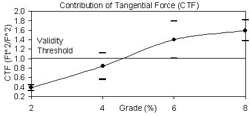
The resulting CTF values for each grade condition are given in Figure 3. For each grade, the average CTF value along with standard deviation error bars are given. All of the grade conditions were found to be statistically different except for between the 6% and 8% grades. The average of the CTF values at the 2% grade was 0.38, within the range of values reported previously for similar conditions [1,2]. CTF values steadily increased through the 6% grade and then began to level off to 1.59 on the 8% grade. CTF values in excess of 1.0 imply that the tangential component of force exceeds the total magnitude of force on the handrim, which is physically impossible.
 |
|---|
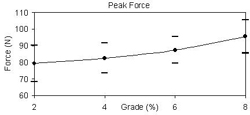
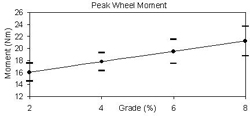
In an effort to better understand the rationale for the CFT values exceeding 1.0, the peak resultant force and wheel moment (CTF input variables) were determined for each grade condition (Figures 4 & 5). It can be seen that both the peak force and moment increase with increasing grade. However, the peak force increased by 21% when transitioning from the 2% to the 8% grade, while the peak moment increased by 37.5%. It is clear that the wheel moment was increasing at a higher rate than the peak force on the handrim. Since the CTF values are exceeding 1.0 and the wheel moment is increasing faster than the peak force, it can be deduced that the contribution of a hand moment is primarily responsible for the increase in CTF. Contribution of an appreciable hand moment to the total moment on the handrim violates the negligible hand moment assumption that has been traditionally used in determining CTF.
 |
|---|
DISCUSSION
Analyzing CTF during wheelchair propulsion provides insight into the biomechanical nature of wheelchair propulsion. It was hypothesized and concluded in this study that the CTF values increased with increasing grade, but were found to exceed the 1.0 validity threshold on the 6% grade. CTF values in excess of 1.0 were determined to be the result of an increased hand moment applied to the handrim. Based on these results, it can be concluded that users adapt to uphill wheelchair propulsion by applying an appreciable forward rotation hand moment to the handrim .
 |
|---|
From this study it is not clear whether the adaptation is due to the increased force required to push uphill or perhaps due to the decreased speed, since both were changed simultaneously. Future work will address these questions through a multi-grade and multi-speed experiment along with an improved method of determining the CTF. The traditional method of calculating CTF, which assumes a negligible hand moment, does not appear to be valid for uphill propulsion . Future CTF calculations should be based on a Point of Force (POF) estimation, which is not reliant on the negligible hand moment assumption.
REFERENCES
- Boninger,M.L., Cooper,R.A., Baldwin,M.A., Shimada,S.D., and Koontz,A.M. (1999) Wheelchair pushrim kinetics: body weight and median nerve function. Arch Phys Med Rehabil 80, 910-5.
- De Groot,S., Veeger,D.H., Hollander,A.P., and Van der Woude,L.H. (2002) Wheelchair propulsion technique and mechanical efficiency after 3 wk of practice. Med.Sci.Sports Exerc. 34, 756-766.
- De Groot,S., Veeger,H.E., Hollander,A.P., and Van der Woude,L.H. (2002) Consequence of feedback-based learning of an effective hand rim wheelchair force production on mechanical efficiency. Clin.Biomech. 17, 219-226.
ACKNOWLEDGMENTS
This research was funded by the National Center for Medical Rehabilitation Research in the National Institute of Child Health and Human Development at the National Institutes of Health through Small Business Innovation Research Phase II Grant #2 R44 HD36533-02A2.
W Mark Richter
Nashville TN
(615) 837-6902
wrichter@stanford.edu
