Brooke Slavens1-4, Alyssa Paul1-3, Adam Graf4 & Lawrence Vogel4
1Department of Occupational Science & Technology, University of Wisconsin-Milwaukee (UWM), Milwaukee, WI, 2Rehabilitation Research Design and Disability (R2D2) Center, UWM, Milwaukee, WI, 3Orthopaedic and Rehabilitation Engineering Center, Marquette University/Medical College of Wisconsin, Milwaukee, WI, 4Shriners Hospitals for Children, Chicago, IL,
introduction
In 2000, about 88,000 children used a wheelchair, making it the most used assistive mobility device among children under the age of 18. Among these, almost 90% (79,000 children) used manual wheelchairs (Kaye, 2000). More recently, a 2012 Americans with Disabilities Report stated that, as of 2010, 3.7 million Americans used a wheelchair with about 124,000 users under the age of 21 and 67,000 users under the age of 15 (Brault, 2012).
Associated with leading causes of assistive device usage in children and adolescents are severe cases of cerebral palsy (CP), myelomeningocele (MM), spinal cord injury (SCI) and osteogenesis imperfecta (OI). Manual wheelchair use requires the upper extremity (UE) to assume locomotion responsibilities as well as continue to perform other activities of daily living. These tasks imply a load magnitude and frequency the UE is not constructed to handle. Therefore many manual wheelchair users (MWU) (reportedly over 50% of those with SCI) experience UE pain and overuse injuries such as: carpal tunnel syndrome (CTS) (Crane, 2007; Veeger, 1998; Wei 2003). CTS has been reported as one of the most common secondary disabilities amongst wheelchair users, occurring in 50-70% of SCI MWU and increasing with injury duration (Aljure, 1985; Gellman, 1998; Boninger, 1996 & 1997; Wei, 2003). Due to continual wheelchair use, along with greater life expectancy, UE pathologies and pain may reduce or severely limit independent function and quality of life (Crane, 2007).
Better knowledge of UE dynamics during wheelchair propulsion may improve our understanding of the onset and propagation of UE pathologies. This may lead to improvements in wheelchair prescription, design, training, and long-term/transitional care. Thereby, pathology onset may be slowed or prevented, and quality of life restored.
In order to evaluate UE dynamics during pediatric manual wheelchair use, a custom UE biomechanical model was created. This comprehensive model includes accurate representations of segments and joint locations, and a kinetic model to determine UE joint forces and moments. The model is specifically designed for use within the pediatric MWU population.
methods
Biomechanical Model
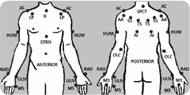 Figure 1: UE model marker set: IJ: suprasternal notch, STRN: xiphoid process, SPC7: spinal process C7, AC: acromioclavicular joint, AI: inferior angle, TS: trigonum spine, SS: scapular spine, AA: acromial angle, CP: coracoid process, HUM: humerus technical marker, OLC: olecranon, RAD: radial styloid, ULN: ulnar styloid, M3 and M5: third and fifth metacarpals.
Figure 1: UE model marker set: IJ: suprasternal notch, STRN: xiphoid process, SPC7: spinal process C7, AC: acromioclavicular joint, AI: inferior angle, TS: trigonum spine, SS: scapular spine, AA: acromial angle, CP: coracoid process, HUM: humerus technical marker, OLC: olecranon, RAD: radial styloid, ULN: ulnar styloid, M3 and M5: third and fifth metacarpals.The bilateral UE model comprises 11 segments: thorax, clavicles, scapulae, upper arms, forearms and hands. The joints of interest are: three degree-of-freedom wrist, glenohumeral (GH) and acromioclavicular (AC) joints; and two degree-of-freedom elbow and sternoclavicular (SC) joints. Twenty-seven passive reflective markers are placed on bony anatomical landmarks to reduce skin motion artifact while defining the aforesaid segments (Figure 1).
Joint axes are embedded at the joint centers which are calculated using subject specific anthropometric data. A Z-X-Y Euler angle sequence is used to determine the joint angles of the distal segment with respect to the proximal segment. Following ISB recommendations: the Z-axis points laterally towards the subject’s right side, the X-axis points anteriorly and the Y-axis points superiorly (Wu, 2005).
Several design features were developed in order to best define shoulder complex kinematics, quantify UE joint kinetics and have greatest anatomical accuracy. First, to avoid possible marker contact with the wheelchair during propulsion, a single marker was placed on the olecranon, a method previously validated by Hingtgen et al. (Hingtgen, 2006). Next, the marker set used to describe the thorax was designed to more closely reflect the model described by Nguyen et al. in which a direct method of marker placement on thorax landmarks reduces the influence of shoulder girdle movement on thoracic kinematic measurements (Nguyen, 2005). In order to assure the greatest accuracy the method of determining the glenohumeral joint center location was designed using regression equations developed by Meskers et al. that employ the positions of five scapula markers (Meskers, 1998).
Additionally, with the inclusion of the scapula segments, a new marker tracking method for the TS and AI scapula markers is used to reduce the effects of skin motion artifact and possible marker-wheelchair interaction, using techniques as developed by Senk et al. (Senk, 2010).
Body segment parameters, required in the Newton-Euler equations of motion for joint force and moment determination, were calculated through equations developed specifically for the pediatric and adolescent populations. Equations by Jensen et al. (Jensen, 1989) determine the mass proportion of the segment to the body for the hands, forearms and upper arms, using the subject’s age (in years) as the independent variable. Also utilized was Jensen et al.’s polynomial regression equations developed based on age (for subjects ages 4 to 20) for the calculation of the location of the segment center of mass. Lastly, in order to determine the segment’s inertias, equations developed by Yeadon et al. were applied to each subject, requiring many subject specific measurements (Yeadon, 1989).
The SmartWheel, produced by Out-Front (Mesa, AZ, USA), was used to record kinetic data during wheelchair propulsion. The SmartWheel utilizes voltage changes in six strain gauges placed on specialized wheel spokes to calculate the three forces and three moments as applied by the hand to the wheelchair handrim. This data was used in the Newton-Euler equations of motion in order to determine the forces and moments at each UE joint of interest through the inverse dynamics method (Zatsiorsky, 2002).
Matlab (MathWorks, Inc., Massachusetts, USA) was used for model development. Further model details may be found in the IEEE EMBS 2012 conference proceedings (Paul, 2012). Matlab and Microsoft Excel (2010) were used for data analysis.
Protocol
The pediatric biomechanical model was implemented at Shriners Hospital for Children – Chicago for analysis of manual wheelchair mobility. Two adolescent males with SCI were evaluated. Subject one was 17 years of age and diagnosed with a C6, AIS B level, SCI resulting in limited grasp and the use of friction cuffs during propulsion. Subject two was 18 years of age and diagnosed with a T1, AIS B level, SCI, with no UE limitations. The subjects propelled their wheelchair along a 15 meter walkway at a self-selected speed for multiple trials, with adequate rest provided between trials. Motion data was collected at 120Hz using a 14 camera Vicon MX motion capture system. Simultaneous force and moment data occurring at the hand-handrim interface was also collected at 240 Hz using a SmartWheel (Out-Front, Mesa, AZ). The SmartWheel replaced the subject’s own wheel on the dominant side; both subjects were right-hand dominant.
The thorax and wrist, elbow, GH, AC and SC joint kinematics as well as wrist, elbow and GH joint kinetics were determined in all three planes of motion: sagittal, coronal and transverse. Data was normalized to 100% percent stroke cycle and processed every 1%. The stroke cycle was defined to include both the push and recovery phases, with 0% representing the onset of propulsive moment about the axle. To compare subject data the forces were normalized to the subject’s body weight (%BW) and the moments were normalized to the subject’s body weight and height (%BWxH). Subjects’ right wrist kinematic and kinetic data was found to be most clinically significant and is presented here. T-tests were used for statistical comparisons between subjects.
results
Mean wrist joint angles, forces and moments characterized over the wheelchair stroke cycle in each plane of motion, along with +/- one standard deviation are depicted in Figure 2 for each subject. The mean peak angles, forces and moments, their locations during the stroke cycle and ranges of motion (ROMs) were also computed over the stroke cycle.
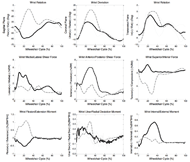 Figure 2: Mean (bold) and +/- 1 SD (dashed) wrist joint angles, top row (subject 1: solid black, subject 2: dashed gray). Wrist joint forces and joint moments are depicted in the middle and bottom rows, respectively. Data reported for subjects’ right-hand (dominant) side.
Figure 2: Mean (bold) and +/- 1 SD (dashed) wrist joint angles, top row (subject 1: solid black, subject 2: dashed gray). Wrist joint forces and joint moments are depicted in the middle and bottom rows, respectively. Data reported for subjects’ right-hand (dominant) side.Differences between the two subjects are easily seen in sagittal plane wrist motion, with subject 1 exhibiting large extension angles throughout the stroke cycle, while subject 2 approaches a neutral position. Subject 1 experienced greater shear forces (laterally and anteriorly directed) and an internal moment, while subject 2 experienced a greater inferiorly directed force and a flexion moment. A major difference between subjects is the occurrence of maximum wrist extension of subject 1, -60.2°, and minimum wrist extension of subject 2, -5.1°, occurring at similar points in the stroke cycle, 24% and 32%, respectively. Similar closely occurring “opposites” may be seen in superior/inferior wrist forces (subject 1: 3.8%BW tension at 20.2% and subject 2: -8.3%BW compression at 29.5%) and flexion/extension moments (subject 1: -0.58%BWxH extension at 23.0% and subject 2: 1.16%BWxH flexion at 22.3%).
Both subjects showed similar transition points from the push phase to the recovery phase of the stroke cycle, though they were significantly different (p<0.05). They occurred, on average, at 52.6% stroke cycle for subject one and slightly earlier at 48.2% stroke cycle for subject two.
There were a number of statistically significant differences between the subjects. The peak wrist ulnar deviation was significantly different (p<0.01) with 8.9° for subject one and 21.0° for subject two. Peak lateral force was 5.9%BW for subject one and 2.3%BW for subject two (p<0.01). Peak anterior force for subject one was 6.7%BW and for subject two 2.7%BW (p<0.01). Lastly, the peak internal moments were significantly different (p<0.01) with 0.77%BWxH for subject one and 0.27%BWxH for subject two. Additionally, sagittal plane and coronal plane ROMs as well as all force ranges and flexion/extension and internal/external moment ranges were found to be significantly different (p<0.01) between subjects.
discussion
The custom pediatric UE biomechanical model successfully quantified joint dynamics in two adolescent MWUs with SCI. Three-dimensional UE joint angles, joint forces and joint moments were characterized. These data demonstrate two main points. First, different levels of SCI may have great effect on both kinematic and kinetic joint demands during manual wheelchair propulsion, as seen with these two subjects. Secondly, despite the differences exhibited between the two subjects, the wrist kinematic and kinetic peaks for both subjects were experienced primarily in the 20-30% stroke cycle range. This highlights an area of high joint demand during the push phase of the stroke cycle that should be further investigated. Additionally, the fact that both subjects incur excessive wrist joint motions almost simultaneously with peak wrist joint forces and moments is concerning given the extremely repetitive nature of wheelchair propulsion. With regards to long-term pain and subsequent pathology, this may be indicative of the high rate of carpal tunnel syndrome amongst MWU.
conclusion
Results of this work may aid clinicians in better understanding wheelchair mobility through improved quantitative characterization and support clinical prescription, training and therapeutic decision making for pediatric MWUs. This work may be used to provide quantitative data to support alternative mobility technology, movement patterns or assistive devices for children with orthopaedic disabilities. Outcomes from this research supported a push-activated power assist wheelchair for subject one. Further research is underway to investigate wheelchair dynamics of the shoulder complex, elbow, and wrist joints with pediatric subjects of varying ages and pathologies and their correlation to pain and functional outcomes.
References
Aljure, J., Eltorai, I., Bradley, W.E., Johnson, B. (1985). Carpal tunnel syndrome in paraplegics. Paraplegia, 23, 182.
Boninger, M.L., Cooper, R.A., Robertson, R.A., Rudy, T.E. (1997). Wrist biomechanics during two speeds of wheelchair propulsion: an analysis using a local coordinate system. Arch Phys Med Rehabilil, 78, 364-72.
Brault, M.W. (2012). Americans with Disabilities: 2010. Current Population Reports, P70-P131, U.S. Census Bureau, Washington, DC.
Crane, B. (2007). In M.M. Lusardi, and C. C.Nielsen (Ed. 2nd) Orthotics and Prosthetics in Rehabilitation (pp. 489-516). St. Louis, MS: Saunders Elsevier.
Gellman, H., et al. (1993). Carpal tunnel syndrome in paraplegics: a study of carpal tunnel pressures. J. Bone Jnt. Surg. 70(4), 517–519.
Hingtgen, B., McGuire, J.R., Wang, M., Harris, G.F. (2006). An upper extremity kinematic model for evaluation of hemiparetic stroke. Journal of biomechanics, 39(4), 681-8.
Jensen, R. K. (1989). Changes in segment inertia proportions between 4 & 20 years. Journal of Biomechanics, 22(6/7) 529-36.
Kaye, H. S., Kang, T., LaPlante, M.P. (2000). Mobility Device Use in the United States. Disability Statistics Report, Washington, DC: US Dept Education, NIDRR. 14, 1-60.
Meskers, C. G., Van Der Helm, F.C., Rozendaal, L.A., & Rozing, P.M. (1998). In vivo estimation of the glenohumeral joint rotation center from scapular bony landmarks by linear regression. Journal of biomechanics, 31(1), 93-6.
Nguyen T. C., & Baker, R. (2004). Two methods of calculating thorax kinematics in children with myelomeningocele. Clinical biomechanics (Bristol, Avon), 19(10), 1060-5.
Paul, A., et al. (2012). Upper extremity biomechanical model for evaluation of pedicatirc joint demands during wheelchair mobility. In Proceedings of the IEEE EMBS Annual Conference, San Diego, CA.
Robertson, R. N., Boninger, M.L., Cooper, R.A., Shimada, S.D. (1996). Pushrim forces and joint kinetics during wheelchair propulsion. Arch Phys Med Rehabil, 77(9), 856-64.
Šenk M., & Chèze, L. (2010). A new method for motion capture of the scapula using an optoelectronic tracking device: a feasibility study. Computer methods in biomechanics and biomedical engineering, 13(3), 397-401.
Slavens, B., et al. (2011). Upper extremity wheelchair kinematics in children with spinal cord injury. In Proceedings of the IEEE EMBS Annual Conference, Boston, MA.
Veeger, H.E., Meershoek, L.S., van der Woude, L.H., Langenhoff, J.M. (1998). Wrist motion in handrim wheelchair propulsion. J. Rehabil. Res. Dev. 35, 305–313.
Wei, S., Huang, S.L., Jiang, C., Chiu, J. (2003). Wrist kinematic characterization of wheelchair propulsion in various seating positions: implications to wrist pain. Clinical Biomechanics, 18(6), S46-S52.
Wu, G., et al. (2005). ISB recommendation on definitions of joint coordinate systems of various joints for the reporting of human joint motion--Part II: shoulder, elbow, wrist and hand. Journal of Biomechanics, 38, 981-92.
Yeadon, M. R. & Morlock, M. (1989). The appropriate use of regression equations for the estimation of segmental inertia parameters. Journal of Biomechanics, 22(6/7), 683-89.
Zatsiorsky, V. M. (2002). Kinetics of Human Motion. Champaign, IL: Human Kinetics.
Acknowledgements
We would like to acknowledge the Department of Education NIDRR grant H133E100007. However, the contents of this work do not necessarily represent the policy of the Department of Education, and you should not assume endorsement by the Federal Government.