I INTRODUCTION

Recent statistics estimate that stroke became among the first causes of death in North America [1]. Every year, stroke kills about 130 000 of 800 000 Americans who die because of a cardiovascular disease, and around 610 000 people suffer a stroke [2]. The most common symptom of a stroke is sudden impairment or numbness of the face, arm or leg. The stroke victim finds difficult to assess the distance, the position and the speed of movement [3]; that results in the inability to perform activities of daily living.

Rehabilitation programs are the best method to help stroke victims to recover their lost capacity and acquire new skills [3]. The stroke patient must be subjected to those programs very quickly, during the first months following the stroke accident or brain attack because the improvement becomes slower over time [3]. In recent years, a new method of rehabilitation based on robotics applications has been gaining a lot of attention among the research community. This method relies mainly on the capability of the robot to repeat precisely the medical tasks (such as a rehabilitation exercise) for longer periods of time allowing a theoretical infinite repetition of the rehabilitation exercises.

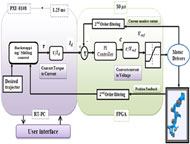
Many groups of researcher have developed exoskeleton robots, for instance, InMotion [4] have two degree of freedom 2DOFs, assisted rehabilitation and measurement guide (ARMin) [5] have 6DOFs, intelligent Pneumatic Arm Movement (iPAM) [6] have 5DOFs. These robots are connected to the subject upper-limb. The patient can move his arm in the workspace depending on the available degrees of freedom of the robot [7]. To assist stroke patients with dysfunctional upper limb function we have created a new 7DOFs exoskeleton robot called ETS-MARSE (Motion Assistive Robotic-exoskeleton for Superior Extremity) [8]. It can perform a large range of movements (Table I) and is able to effectively provide passive and active rehabilitation therapy.

To maneuver the robots to provide rehabilitation therapy many control techniques have been developed, from a simple PID controller to nonlinear control; even intelligent controllers. Many approaches that combine different advanced control techniques had appeared. Between them we can mention: the adaptation of the dynamic parameters using fuzzy controller based on sliding mode control proposed in [9]. This approach is aimed to improve the performance of the robot and limit the chattering problem caused by the discontinuous sign function term, defined as high-frequency activity control signal [10]. An adaptive control based on neural network is presented in [11] to estimate the uncertain parameter and external disturbances. However, the intelligent control as fuzzy logic and neural network controllers have a slow response time as the advanced nonlinear technique requires hulking computations [8]. The virtual decomposition control (VDC) in [12] provides satisfactory results both at trajectory tracking, and estimation and rejection of the uncertain parameters and external disturbance. There are also a lot of methods using robust controllers [13] to deal with friction uncertainties caused by the high-order dynamic models of the robots. We also need to consider the variations of upper-limb mass of different patients as external perturbation that produce problems in control of high-dynamic robots, as the ETS-MARSE, and affect the tracking performance of the robot. For this reason we developed a new control technique that combines two robust control strategies. Firstly, the sliding mode controller which can ensure perfect tracking despite model uncertainties and external perturbations [8]. To eliminate the chattering problem, we replaced the sign function with a saturation function [14]. Secondly, the backstepping control that permits to design a control law in several steps which ensures the global stability of the exoskeleton robot [15].

To evaluate the robustness of the controller we have implemented trajectory tracking corresponding to recommended passive rehabilitation tasks [10]. All the experiments were conducted with healthy subjects to provide passive functional therapy. In the next section, the kinematics and workspace of ETS-MARSE robot are presented and. the control approach is described. Experiment results will be presented in section III, and finally the conclusion and future works in section IV.

II CONTROL DESIGN

A. ETS-MARSE robot

The modeling of the exoskeleton was done based on the joints and movements of the human upper limb. In the model shown in Fig.1, joints one, two and three represent the scapulohumeral joint (shoulder joint). Joints one and two correspond respectively to the horizontal and vertical extension /flexion of the shoulder joints, while joint three corresponds to the external/internal rotation of the shoulder joint. Joint four corresponds to the flexion/extension of the elbow joint. The joint five represents supination pronation of the forearm and joints six and seven correspond respectively to ulnar/radial deviation, and flexion/extension of the wrist joint. The workspace of the exoskeleton is presented in Table I. The kinematic analysis of the exoskeleton ETS-MARSE is based on the frames [16] attached as shown in Fig. 1.

B. Control

The approach of the sliding mode- backstepping control is presented for the dynamic of the exoskeleton ETS-MARSE. The dynamic behavior of the ETS-MARSE can be expressed as:

$$M(\Theta )\ddot{\Theta }+C(\Theta ,\stackrel{\cdot }{\Theta })\stackrel{\cdot }{\Theta }+G(\Theta )+F(\Theta ,\stackrel{\cdot }{\Theta })=\tau$$                      (1)

TABLE I Movements of ETS-MARSE

Joints	Motion	Workspace
1	Flexion/Extension	0°/140°
2	Abduction/Adduction	140°/0°
3	Internal/external Rotation	-85°/+75°
4	Flexion/Extension	120°/0°
5	Pronation / Supination	-85°/+85°
6	Ulnar / Radial deviation	-30°/+20°
7	Flexion/Extension	+60°/-50°

where $\Theta \in {\mathbb{R}}^7$ is the joint angles vector, $M(\Theta )\in {\mathbb{R}}^{7\mathrm{x7}}$ is the inertia matrix, $C(\Theta ,\stackrel{\cdot }{\Theta })\in {\mathbb{R}}^7$ is the Coriolis/centrifugal matrix, $G(\Theta )\in {\mathbb{R}}^7$ is the gravity vector, τ is the generalized torques vector and $F(\Theta ,\stackrel{\cdot }{\Theta })$ is the friction vector. Note that the friction vector is considered as a non-linear Coulomb friction and can be written as:

$F(\Theta ,\stackrel{\cdot }{\Theta })={\tau }_{\mathrm{friction}}=\mathrm{cf}\ast \mathrm{sign}(\stackrel{\cdot }{\Theta })$                                     (2)

where cf is the constant of Coulomb-friction. Equation (1) can be written as:

$$\ddot{\Theta }={M(\Theta )}^{-1}\tau -{M(\Theta )}^{-1}[(C(\Theta ,\stackrel{\cdot }{\Theta })\stackrel{\cdot }{\Theta }+G(\Theta )+F(\Theta ,\stackrel{\cdot }{\Theta })]$$   (3)

Since $M(\Theta )$  is symmetrical and positive definite ${M(\Theta )}^{-1}$ always exists.

The philosophy of sliding mode control is first, to attract the states of the system in a desired surface; then, design a control law that keeps the system in this surface. The control law is divided in two terms [17]:

$$\tau ={\tau }_{\mathrm{Sliding}}+{\tau }_{\mathrm{Nominal}}$$                                                       (4)

where, ${\tau }_{\mathrm{Sliding}}$  is a nonlinear term used to compensate uncertain model parameters and ${\tau }_{\mathrm{Nominal}}$  is the nominal control determined by the model of the robot [17]. ${\tau }_{\mathrm{Sliding}}$  will be calculated by sliding mode approach and ${\tau }_{\mathrm{Nominal}}$  will be computed by the backstepping approach that permits to design the control law in several steps based on a certain Lyapunov function candidate defined positive and which derivative is always negative [15].

The first step in this approach is to select the sliding surface using the dynamic of the errors. We can define the sliding surface as following:

$$e_1=\Theta -{\Theta }_d$$                                                                  (5)

$$S=e_2=\stackrel{\cdot }{\Theta }-{\gamma }_1$$                                                          (6)

where, ${\Theta }_d=\left[{\Theta }_{1d}......{\Theta }_{\mathit{7d}}\right]$  is the desired trajectory for all joints and ${\gamma }_1$  is a virtual control term defined as:

$${\gamma }_1={\stackrel{\cdot }{\Theta }}_d-k_1{e}_1$$                                                             (7)

where $k_1$  is a 7x7 diagonal positive-definite matrix. Considering the Lyapunov function candidate:

$$V_1=\frac{1}{2}{S}^{T}S$$                                                                      (8)

The derivative of $V_1$  is:

$${\stackrel{\cdot }{V}}_1=e_2^T\stackrel{\cdot }{s}$$                                                                         (9)

Choosing $\stackrel{\cdot }{s}$  as:

$$\stackrel{\cdot }{s}=-k_2\mathrm{sign}(s);t,k_2>0\Rightarrow \stackrel{\cdot }{V}<0$$                          (10)

with,

$$\mathrm{sign}(s)=\begin{cases}1 & \text{if $\mathrm{for}s>0$}\\ 0 & \text{if $\mathrm{for}s=0$}\\ -1 & \text{if $\mathrm{for}s<0$}\end{cases}$$                                          (11)

where $k_2$  is a 7x7 diagonal positive-definite matrix. Then relation (13) ensures the stabilization of ${\stackrel{\cdot }{V}}_1$ .

It is to be noted that ${\tau }_{\mathrm{Sliding}}=k_2\mathrm{sign}(s)$  is a discontinuous term and it gives high control activity that causes the phenomenon known as chattering. This problem could produce damage in the motors. We found in the literature a way to transform this discontinuous term to a continuous term defined as ${\tau }_{\mathrm{Sliding}}=k_2\mathrm{sat}\left(\raisebox{1ex}{$s$}\!\left/ \!\raisebox{-1ex}{$\varnothing $}\right.\right)$ ], with:

$$\mathrm{sat}\left(\raisebox{1ex}{$s$}\!\left/ \!\raisebox{-1ex}{$\varnothing $}\right.\right)=1\mathrm{for}s\ge \varnothing ,\raisebox{1ex}{$s$}\!\left/ \!\raisebox{-1ex}{$\varnothing $}\right.-\varnothing \le s\le \varnothing t,0<\varnothing \ll 1,-1\mathrm{for}s\le \varnothing$$        (12)

 

The nominal control designed by backstepping approach can be presented as follows. Consider the Lyapunov function candidate:

$$v_2=\frac{1}{2}{e}_1^T{e}_1$$                                                                  (13)

Differentiating equation (10) with respect to time yields:

$${\stackrel{\cdot }{e}}_1=e_2+{\gamma }_1-{\stackrel{\cdot }{\Theta }}_d$$                                                            (14)

The derivative of $V_2$  is given by:

$${\stackrel{\cdot }{V}}_1=e_1^T{\stackrel{\cdot }{e}}_1$$

$$=e_1^T\left(e_2+{\gamma }_1-{\stackrel{\cdot }{\Theta }}_d\right)$$                                                     (15)

Substituting equation (18) in equation (19) we obtain:

$${\stackrel{\cdot }{V}}_2=e_1^T{e}_2+e_1^T{\stackrel{\cdot }{\Theta }}_d-e_1^T{k}_1{e}_1-e_1^T{\stackrel{\cdot }{\Theta }}_d$$  

$${\stackrel{\cdot }{V}}_2=-e_1^T{k}_1{e}_1+e_1^T{e}_2$$                                                     (16)

The first term of equation (20) is stable and the stability of second term will be demonstrated next. Differentiating equation (10) with respect to time yields:

$${\stackrel{\cdot }{e}}_2=\ddot{\Theta }-{\stackrel{\cdot }{\gamma }}_1$$

$${\stackrel{\cdot }{e}}_2=M{\left(\Theta \right)}^{-1}\tau -M{\left(\Theta \right)}^{-1}\left[\left(C\left(\Theta ,\stackrel{\cdot }{\Theta }\right)\stackrel{\cdot }{\Theta }+G(\Theta )+F\left(\Theta ,\stackrel{\cdot }{\Theta }\right)\right)\right]-{\stackrel{\cdot }{\gamma }}_1$$                                                                        (17)

where, ${\stackrel{\cdot }{\gamma }}_1={\ddot{\Theta }}_d-k_1{\stackrel{\cdot }{e}}_1$ . Consider the Lyapunov function candidate:

$$V_3=V_1+V_2+\frac{1}{2}{e}_2^{T}M\left(\Theta \right)e_2$$                                          (18)

The derivative of $V_3$  is given by:

$${\stackrel{\cdot }{V}}_3={\stackrel{\cdot }{V}}_1+{\stackrel{\cdot }{V}}_2+\frac{1}{2}{e}_2^{T}M\left(\Theta \right){\stackrel{\cdot }{e}}_2+\frac{1}{2}{e}_2^T\stackrel{\cdot }{M}\left(\Theta \right)e_2$$                    (19)

Lemma 1: the derivatives of the inertia matrix $M\left(\Theta \right)$  with the matrix $C\left(\Theta ,\stackrel{\cdot }{\Theta }\right)$  satisfy [18]:

$${\gamma }^T\left[\stackrel{\cdot }{M}\left(\Theta \right)-2C\left(\Theta ,\stackrel{\cdot }{\Theta }\right)\right]y=0,y,\Theta ,\stackrel{\cdot }{\Theta }\in R^n$$              (20)

Using this lemma we obtain:

$${\stackrel{\cdot }{V}}_3=-e_1^T{k}_1{e}_1+e_1^T{e}_2-e_2^T{k}_2\mathrm{sat}\left(\frac{s}{\varnothing }\right)+e_2^T\left(\tau -C\left(\Theta ,\stackrel{\cdot }{\Theta }\right)\stackrel{\cdot }{\Theta }-G\left(\Theta \right)-F\left(\Theta ,\stackrel{\cdot }{\Theta }\right)\right)-e_2^T\stackrel{}{M}\left(\Theta \right)++\frac{1}{2}{e}_2^T\stackrel{\cdot }{M}\left(\Theta \right)e_2$$

$${\stackrel{\cdot }{V}}_3=-e_1^T{k}_1{e}_1+e_1^T{e}_2-e_2^T{k}_2\mathrm{sat}\left(\frac{s}{\varnothing }\right)+e_2^T\left(\tau -C\left(\Theta ,\stackrel{\cdot }{\Theta }\right){\gamma }_1-G\left(\Theta \right)-F\left(\Theta ,\stackrel{\cdot }{\Theta }\right)+\stackrel{}{M}\left(\Theta \right){\stackrel{\cdot }{\gamma }}_1\right)$$           (21)

Consider the control law that stabilizes the system as follows:

$$\tau =-k_3{e}_2-e_1+C\left(\Theta ,\stackrel{\cdot }{\Theta }\right){\gamma }_1+G\left(\Theta \right)+F\left(\Theta ,\stackrel{\cdot }{\Theta }\right)+\stackrel{}{M}\left(\Theta \right){\stackrel{\cdot }{\gamma }}_1+k_2\mathrm{sat}\left(\frac{s}{\varnothing }\right)$$                                       (22)

where $k_3$  is a 7x7 diagonal positive-definite matrix.

Substituting equation (22) in equation (21), we find:

$${\stackrel{\cdot }{V}}_3-e_1^T{k}_1{e}_1-e_2^T{k}_3{e}_2$$ .   

III-EXPERIMENTS AND RESULTS

The control of the exoskeleton ETS-MARSE robot was implemented in LabView (National Instruments) PXI system. A PXI card performs the joint-based control and was used as the robot operating system. The control architecture and experimental setup for the ETS-MARSE is designed in three blocks shown in Fig. 2. First, the user interface is connected to the ETS-MARSE for selection of the control technique and the predetermined rehabilitation exercise (desired trajectory); it also feedbacks the experimental data from the robot system to analyse the exoskeleton performance. The second block is the PXI-8108, where the Sliding mode-Backstepping control was implemented with a period of 1.25 ms. The controller output is the torque to the joints; this torque was transformed to current and then to desired voltages to command the motor drivers [10]. Finally, a FPGA (field programmable gate array) is programmed to run two loops simultaneously. The first loop contains a simple (PI) control for the current of the motors, according to the current reference calculated. The second loop contains a code to obtain the position based on Hall sensors. The FPGA has a sampling time of 50 μs.

In this paper, experiments were performed with four healthy human subjects (weight: 65-95 kg; age: 27-55 years; height: 168-186 cm). We choose in these tests two passive rehabilitation exercises to increase muscle power and joint range of movement of people with impaired upper limb motion. The control gains used for the tests were found experimentally as follows:

$$k_1=\mathrm{diag}\left[15151515151515\right]$$  

$$k_2=\mathrm{diag}\left[39203825384650\right]$$

$$k_3=\mathrm{diag}\left[130150150150200180200\right]$$  

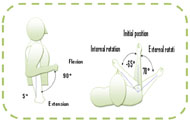
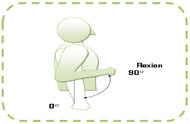
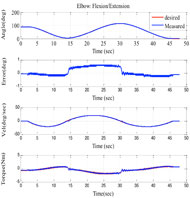
The first passive exercise depends on one joint only (elbow joint flexion/extension). The joint started from an initial position of 90°, goes to 5° and return to initial position with a maximum speed of 45°/sec. The exercise is shown in Fig. 3.

The experimental results of the task performed with subject-A (age: 30 years; height: 177 cm; weight: 75 kg) are shown in Fig. 4. It is clear from the figure that the performance of the sliding mode-backstepping control was very good, with dynamic error less than 0.8° (2nd row of the figure). Further, to validate the robustness of the controller, the same task was conducted with subject-B (age: 27 years; height: 170 cm; weight: 79 kg). We observed from the experimental results illustrated in Fig. 5, that the controller showed excellent tracking performance; although the mass of the arm changed, the tracking error stayed less than 0.5°. It is apparent from the plot of velocity (3rd row of the figure) that the controller gave smooth tracking; this means that the change of the arm mass did not affect the control and the performance of the robot.

The second trajectory is a basic passive rehabilitation exercise based on two joints (elbow joint flexion/extension and shoulder joint internal/external rotation). It started for the elbow joint at an initial position of 90°, going to 5° and return to initial position with speed varying between 20°/sec and -20°/sec. After that, the shoulder joint (joint 3) started from initial position of 0°, rotated to 70° towards external rotation and returned to -65° towards internal rotation with speed varying between 45°/sec and -45°/sec. The movement can be seen in Fig. 6.

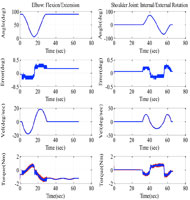
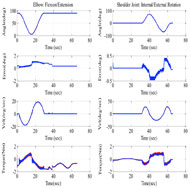
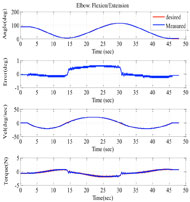
The experimental results of simultaneous elbow and shoulder joints movement performed with subject-C (age: 55 years; height: 168 cm; weight: 65 kg) are shown in Fig. 7. It is clearly appreciable from the figure that the tracking performance of the controller was excellent; where the tracking error (2nd row of the figure) was less than 0.5°. To further proof the robustness of the proposed control, the same exercise was conducted with subject-D (age: 45 years; height: 186 cm; weight: 95 kg). Form Fig. 8 we can easily see that the measured trajectories overlap with the desired trajectories with tracking error less than 1.0° for elbow joint and 0.5° for shoulder joint. We observe that the error increased in the first sequence of experiment (Fig. 8) because the mass of the arm changed; after that, the controller corrected the state and the error decreased to 0.5°. It is obvious from the plot of velocity (3rd rows of the figure) that the controller gave smooth tracking and behaved correctly despite the changes in the mass of the arm.

IV-CONCLUSION

In this paper, we present a new controller based on sliding mode–backstepping control to manipulate an exoskeleton called ETS-MARSE to be able to perform passive rehabilitation exercises. This therapy allows healthy subjects to perform any pre-defined trajectory. All desired trajectories were tested with different subjects to demonstrate the robustness of the controller. Experimental results showed an excellent tracking performance and demonstrated the efficient of the control to deal with different subjects’ masses. In future works, we will develop intelligent control methods to provide active rehabilitation and assistance therapy and improve the performance of the robot.