INTRODUCTION

The most important sense for grasping and manipulating objects safely and efficiently is the tactile sense: individuals with an impaired sense of touch at the fingers often drop or crush objects [1]. This is not true for vision where we often complete grasping and manipulation tasks successfully when vision is occluded or reduced. Touch also efficiently gathers important information from the environment [2], such as friction, for object recognition and manipulation. The lack of tactile sensation in commercial hand prostheses also results in individuals using significant visual attention resources for what were originally simple tasks in the intact hand. The addition of sensory feedback about tactile information and the reduced need for visual attention are two of the most desired requirements for upper limb prostheses [3].

Tactile information can be relayed through the use of visual, auditory or tactile displays. In some sense, visual or auditory feedback is advantageous due to the large number of affordable and sophisticated commercially available displays. However, these modalities are often engaged in obtaining other relevant information from the environment for the tasks being performed. Although each modality is thought to have their own working memory, the amount is limited for each modality [4]. With no external feedback needed for touch to sense when focused on a manipulation task with the prosthetic, there is likely to be a significant amount of its working memory still available. For tactile feedback, while much of the tactile information needed during grasping and manipulation is normally processed unconsciously by the brain, it is unlikely that this can occur when the feedback site is removed from the site of action, as is the case for prostheses. Instead we will consider using an easily understood tactile property, roughness, as a proxy for the tactile information. This will also allow switching between dimensions of tactile information (e.g., grasp force, temperature) as is relevant during the task.

It is known that both electrical and mechanical skin stimulation can increase the performance and the user’s acceptance of a prosthetic hand [5]. In this paper, we consider mechanical skin stimulation as it more easily provides consistent percepts and is considered more acceptable than electrotactile feedback. Direct neural interfaces do exist but still have issues of stability over their lifetime [6]. For mechanical skin stimulation, we will use vibrotactile feedback due to its ability to be implemented with small, low cost vibrators that are commonly found in smartphones (such as linear resonant actuators or eccentric rotating mass motors). In previous work [7], we found that using frequency as the display parameter over a range of 0 Hz to 100 Hz was effective. However, vibration motors, such as linear resonant actuators (LRAs) or eccentric rotating mass motors (ERMs), either have a limited frequency range (LRAs) or frequency is confounded with amplitude variations (ERMs). We will instead consider the use of modulating the amplitude of a LRA acting at its resonant peak with a square wave of varying frequency.

Previous work has only examined the potential of using AM modulation frequency as a display parameter to a limited degree and only on the fingertip [7,8].  In addition, published work describing the relationship of pure frequency to roughness has indicated that there may not be a one to one mapping [9].  In this paper, we examine the relationship between AM modulation frequency and roughness for three body sites: the pad of the fingertip, the ventral surface of the forearm and the skin surface over the bicep. The latter two sites were chosen due to their common use as tactile feedback sites for prosthetics. In order to obtain an accurate understanding that can be applied across devices despite their different characteristics, we will hold the amplitude of the signal constant at 30 dB SL (perceptual magnitude).

METHODS

Apparatus and Stimuli

The experiment was performed with a C3 tactor (Engineering Acoustics, Inc.) providing vibrotactile signals while secured to each subject’s second digit finger pad, ventral part of the forearm or the skin surface above the bicep. These sites correspond to the direct co-location of the feedback with the finger performing the task, approximate placement of myoelectric control for transradial prostheses and approximate placement of myoelectric control for transhumeral prostheses, respectively. For the finger, the tactor was mounted inside of a plastic ring that fit around the finger with an aperture for the contactor to stimulate the skin on the finger pad. For the other two sites, an approximately 4 inch long fabric cuff made out of a stretchable nylon type fiber was provided to secure the tactor just below (2.5 cm) the elbow joint on the ventral side at the midline of the forearm or just above (2.5 cm) the elbow joint on the ventral side at the midline of the bicep.  In all cases the tactor was secure against the skin but without a significant pre-indent. The C3 tactor has a peak frequency at approximately 250 Hz and a bandwidth from 180 to 320 Hz (Engineering Acoustics website, 2017). Signals were provided to the tactor by a LabVIEW data acquisition system (DAQ) and amplified by a current amplifying circuit. Subjects wore headphones while listening to pink noise in order to prevent sounds from the tactor from influencing discrimination between signals.

Participants

There were 8 participants in the study, composed of 4 males and 4 females. Subjects were recruited from a population of convenience, and consisted of undergraduate and graduate students recruited from the VCU School of Engineering, aged 20-30. All subjects had full sensation and unimpaired dexterity in their hands. IRB approval was obtained for this experiment.

Procedure

To determine the relationship between variations in modulation frequency and perceived roughness at the three different body sites (finger pad, forearm and bicep), a two-step process was used. The first step was based on the expectation that perceived magnitude would vary as a function of the modulation frequency analogous to results obtained with varying the frequency of pure sine waves. To ensure we did not confound perceived magnitude with perceived variations due to modulation frequency, we first performed a similar experiment to Verrillo (1969) to determine equal sensation levels. The equal sensation level (SL) that was chosen was 30 dB SL as it was significantly above threshold and easily detected without being irritating. The second part of the process was to determine the perception of roughness as a function of modulation frequency at the 30 dB SL.

Equal Sensation Level for Amplitude Modulated Frequencies

To obtain the equal sensation levels for AM signals, we used a similar study design to Verrillo [10] except we varied the modulation frequency of an AM signal rather than the frequency of a pure sinusoid. For the AM signal, the base frequency was kept constant as a 250 Hz sine wave, while the varied modulation waveform was a square wave. Two pure sinusoidal reference signals (high at 250 Hz and low at 64 Hz) were used to match test signals at 30 dB SL.  Instead of the direct matching procedures used by Verrillo [10] in which subjects adjusted the signal intensities themselves, a staircase method (MOBS) with preset termination criteria was used [11]. This procedure was repeated at the pad of the fingertip, the forearm and the bicep, with their order counterbalanced across participants.

Roughness Magnitude Estimation

In order to characterize the perception of roughness as a function of AM modulation frequency for the three body

sites: the fingertip pad, the forearm and the bicep, different AM signals were presented to the participant and they were asked to rate the roughness of the signal. The signals consisted of a sine wave at the frequency of 250 Hz that was modulated by square waves of frequencies: 0, 6, 12, 24, 48 96 and 124 Hz. The signals generated by each of the modulation frequencies were presented in random order in a block of 7 signals. Eight repetitions of a block were made (each with their own random order) at each of the body sites. The order in which the body sites were tested was counterbalanced across participants. 

For each of the body sites, the vibrator was securely attached as described in the apparatus and stimuli section. Participants were told that they would be asked to rate the roughness of the presented signals on a scale of 1 to 100, with 1 being very smooth and 100 being very rough. They were then presented with a block of signals containing the AM signals with the differing modulation frequencies in random order in order to help the participant determine the anchor points on the scale. They were then presented with each of the eight test blocks, as described above. For each signal, the participant was presented with the vibration for 0.5 seconds and then was asked to rate the roughness of what they felt.

RESULTS

Statistics, including means and standard errors were calculated using SPSS.

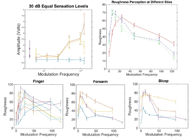
For the mean roughness perception as a function of modulation frequency at the different sites, a line was fit to the data for frequencies greater than and equal to 24 Hz using the function polyfit in MATLAB. The slopes and y-intercept values were, respectively: -0.3810, 71.2372 for the finger, -0.3398, 58.6038 for the forearm and -3619, 65.6678 for the bicep.

DISCUSSION

If mechanical skin stimulation is to be used to convey numeric quantities to the user of a prosthesis, the parameter to be manipulated needs to accurately reflect the value portrayed, i.e., we need to display an accurate scalar quantity where addition or multiplication of the scalar dimension leads to a corresponding addition or multiplication in the percept. It is also of benefit if the quantity can be related to an intuitive description of the mechanical percept, such as roughness. Another property that would be of benefit is using a signal parameter that can be generated with lightweight, low cost motors (such as ERMs or LRAs). In this regard, we examined the use of amplitude modulated signals applied with a C3 tactor. The C3 was selected as we needed a tactor sufficiently strong enough to be perceived at the bicep location. The perceived magnitudes of the waveforms were equalized to ensure that we only were manipulating the modulation frequency and then correlating that parameter with roughness.

For frequencies above 24 Hz, the perceived roughness appears to decrease relatively linearly as a function of modulation frequency at all three sites. We therefore recommend the use of the parameter of AM modulation frequency as a straightforward proxy for any scalar quantity if used at values greater than 24 Hz. Quantitative values for the linear relationship between perceived roughness as a function of modulation frequency are provided in the results section. The steps for displaying scalar information as roughness for a prosthetic user is to: 1) map the quantity onto the roughness scale from 0 to 100, and then 2) use the appropriate values for mapping roughness onto the AM modulation frequency which can be controlled in signal generation.

CONCLUSIONS

This study reveals that a linear relationship exists between AM modulation frequency and perceived roughness at all three body sites, the pad of the index fingertip, the ventral area of the forearm and the skin surface above the bicep, for frequencies greater than a 24 Hz. Parameters are provided so that designers may calculate the mapping for scalar quantities. In future studies, we will use this mapping to provide scalar quantities in tasks that require quantitative values, such as grasping and lifting objects with different frictional coefficients.