A MODEL FOR SIMULATING DYNAMIC CONTROL OF SEATED TRUNK POSTURE USING FUNCTIONAL ELECTRICAL STIMULATION

Ari J Wilkenfeld, PhD, Ronald J Triolo, PhD,
Musa L Audu, PhD
Case Western Reserve University, Cleveland and
VA FES Center of Excellence, Cleveland, Ohio, U.S.A.

In addition to the loss of the ability to stand and walk, paraplegia and tetraplegia often result in a serious detriment in trunk posture when seated. The purpose of this project is to determine the feasibility of a closed-loop functional electrical stimulation (FES) control system for trunk posture for subjects with low cervical or high thoracic spinal injuries. The system would utilize information from sensors for trunk orientation and acceleration and allow users to assume and maintain trunk positions away from the backrest.

To this end, a dynamic model was designed to simulate the effect of FES on the movements of the paralyzed human trunk. The model includes a simplified set of muscles representing those likely to be accessible with surface stimulation (the erector spinae, quadratus lumborum, and rectus abdominus muscles) with properties previously established from cadaver studies in our laboratory. Initial data indicates that reasonable levels of stimulation would allow useful postures using such a system.

restricts an individual’s ability to vary seated position or maintain balance while reaching or manipulating objects in the environment. Moreover, long-term paralysis results in unhealthy postures that lead to skeletal deformities, increases risk for decubitus ulcers, and imposes pressures that compromise internal organ function. The need to address this situation has been largely unexplored by the field of neural prosthetics which has traditionally focused on upper and lower limb function. A variety of researchers have developed dynamic models of the inertial and muscular properties of the human trunk (1,2,3) but none have designed such a model for use to determine control strategies using muscles that are routinely accessed and activated with FES. Such a model is necessary to test any proposed control strategy and to ensure that required postures can be maintained with the muscles that will be available for stimulation.

RESEARCH QUESTION

A large montage of muscles are involved in the stabilization and control of seated trunk posture. In attempting to develop an FES based system to replace the natural neural controller, the first question we had to answer was whether or not we would be able to recruit sufficient force from the muscles available to stimulation (initially using surface stimulators) to maintain the sort of postures that would be required. We used a dynamic model for these purposes.

METHODS

Dynamics Of The Torso

Figure 1: Simplified representation (left) and actual model of the trunk (right)

Since the technique used by a majority of trunk models in the literature- allowing three degrees of freedom at each vertebral joint- is impractical for our purposes, a simplified model of the trunk using only two joints was implemented. As an approximation, the trunk was divided into

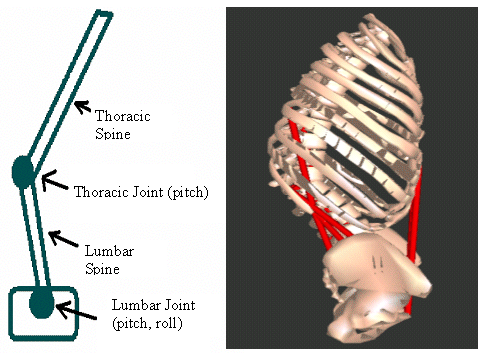three rigid segments: a pelvis, lumbar region, and thoracic region. The lumbar joint has two degrees of freedom (sagittal and lateral bending) whereas the thoracic joint has only one degree of freedom sagittal bending) . Inertial data were calculated assuming that the torso could be approximated as a series of stacked elliptical solids of uniform density and that the relative dimensions of these ellipsoids were approximately the same as those in the male subject in the NIH sponsored “Visible Human” project.

Musculature

Figure 2: Model of trunk with musculature labeled

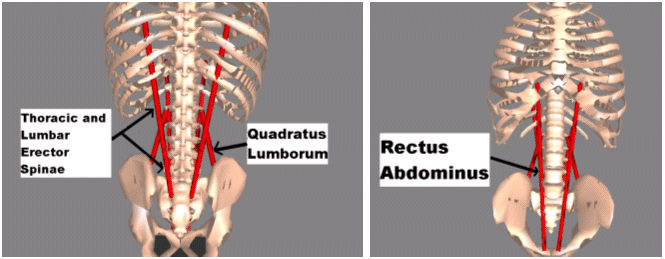Researchers in our lab recently determined the areas, attachment points, and optimal lengths of several major trunk muscle groups going from the pelvis to the thorax- the erector spinae, rectus abdominus, and quadratus lumborum (4). This muscle data were adapted for the two-link torso by giving the erector spinae an attachment on the lumbar spine section and allowing separate levels of activation for the lumbar and thoracic segments of the erector spinae. The maximum muscle forces were calculated assuming a maximum stress of 0.8 MPa (5)

Simulation

Figure 3: Sustainable trunk postures from simulation using full (upper) and half (lower) muscle strength

The model was visualized using the SIMM software package (Musculographics, Inc.) and equations of motion were generated using the SD-FAST package from Symbolic Dynamics, Inc. The inverse dynamic equations were utilized to calculate the required torques about each joint for a given trunk posture and an optimization algorithm was used to minimize the sum of squares of the muscle stresses necessary to maintain those torques. The simulations were run both with the muscles at full strength (to simulate a healthy human torso) and at half strength (a rough approximation of the maximum force that can be elicited from paralyzed muscle using FES).

Results

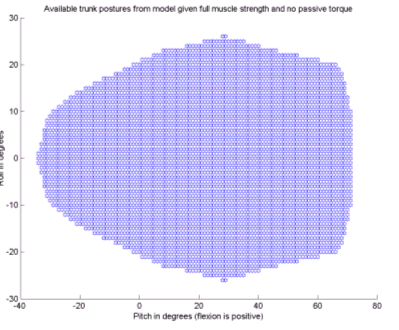
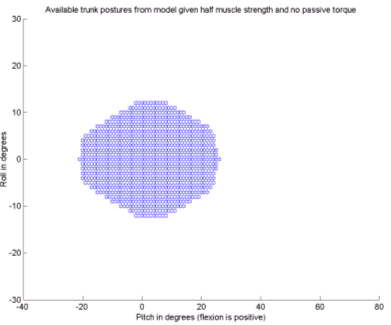
Figure 3 shows the results from the simulations indicating what range of postures can be statically maintained with the available musculature at full and at half strength.

Discussion

As can be seen from the results in Figure 3, while limiting the musculature to half strength significantly limits the available postures, there is still a range of useful postures available. For example, with no lateral bending, an FES based system could allow the patient to have up to 20 degrees of forward reach while still maintaining stability. These results would seem to indicate that further work on such a system is justified. Future work needs to include EMG verification of the model, the addition of a muscle actuated hip joint, a realistic portrayal of passive joint properties, and the development of the control system itself.

References

Acknowledgments

This work was funded by NINDS/NIH postdoctoral training grant contract #1F32NS44700-01 and grant #R01-NS-40547 from the National Institute of Neurological Diseases and Stroke.