Method to Predict Wheelchair Reliability and Lifetime
ABSTRACT
In this paper, we introduce the time-dependent reliability assessment of assistive technologies. It should be stressed that this evaluation takes place at the design stage so as to allow designers and buyers to predict the lifetime of their products before use. Thus, we apply a method from which, we have already shown, good results are obtained for time independent reliability, and upgrade it for reliability evaluation versus time. Then, wheelchair lifetime estimation can be achieved, which is of great interest for people involved in their management.
KEYWORDS
Reliability, Lifetime, Stress/strength approach, Wheelchair design
INTRODUCTION
New assistive technologies, in particular wheelchairs, appear on the market every year. For organisms which prescribe these wheelchairs to disabled people, it is of great interest to know if user needs will be met with these new products and how long they will be satisfied. So far, the only way to qualify a new wheelchair consists in checking whether it passes technical certifications (e.g. the ISO certifications [1]); however they do not give information on the lifetime of the wheelchair.
In this article, we first propose a methodology to help designers and buyers in collaborating to find the most efficient version of a wheelchair. As a result of this methodology, we propose a reliability and lifetime estimation of wheelchair parts for different use scenarios, prior to the product use.
BACKGROUND
Reliability is commonly defined as the probability that a piece of equipment successfully performs its intended function for a given period of time under specified conditions. Reliability estimation is based on the following points: i) it is assumed that user needs have been identified; buyers should list, with users and occupational therapists, the wheelchair functions and the use scenarios associated to customer profiles; ii) designers need to verify that parts involved in the realization of the most important functions are reliable; iii) the failure modes of these parts and their design variables influencing the reliability should be identified.
Several methods in the literature, based on the relation between the failure mode (or the limit state) and the design variable distributions, allow us to calculate reliability. The two most common ones are the FORM/SORM method, which gives results quite quickly, and the Monte Carlo method, which is a more crude, time consuming approach, requiring a lot of simulations [2]. However, they require the knowledge of the probability distribution and its parameters for each of the design variables (such as dimensions, material properties, impacts of manufacturing processes, etc.), and this kind of information is often difficult and expensive to obtain.
Thus, our approach is a good trade off between these two methods. It is based on the Taylor series finite difference calculations and on the stress/strength approach. As this study takes place at the design stage, it should be emphasized that our method asks for low detailed input data, i.e. we only need the mean and the standard deviation for each of the design variables. Moreover, we have already shown in previous work that it gives good results [3]. This method will be described for one wheelchair part, for one chosen failure mode and for a specific scenario.
METHOD
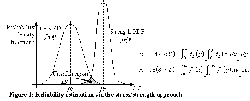 |
|---|
In the traditional design approach, the safety factor is large enough to more than compensate for uncertainties in the value of both the load and the capacity of the system under consideration. With the stress/strength approach, loads and capacities are treated probabilistically [4]. Thus, the expression for reliability 'R' in terms of the random variables 'L' (stress) and 'S' (strength), and their respective probability density functions (PDF), may be illustrated and defined by the following figure (see Figure 1).
Stress identification is conducted by analyzing the load applied to the wheelchair during its use. At the design stage, the wheelchair is modeled on the Pro/Engineer computer aided design system (see Figure 2a). Then, the Adams software based simulation allows the identification of the wheelchair behavior and the efforts of the part under analysis (see Figure 2b). Data are then treated with Stat::Fit which lead to the statistical identification of the stress PDF.
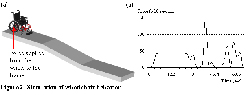 |
|---|
For strength identification, we consider the design variables which influence the behavior of the part being analysed. An analytical model for the chosen failure mode has to be found to define the limit state. It verifies whether the part resists (over the limit state) or not (under the limit state) and gives the strength value. In this study, we implement the following design variables: dimensions, thickness, modulus of elasticity (Young's modulus), material elasticity limits, Wöhler (or S-N) diagram, each of them being described by its mean and its standard deviation. As the number of design variables is large enough, we assume that the strength PDF follows the normal distribution. Then, the Taylor series approximations allow us to reduce the number of simulations, from which we obtain the parameters of the strength PDF, namely its mean and its standard deviation [3]. For each of the simulations, the strength is computed by a code (Maple programmed) based on a finite element procedure.
Once both stress and strength PDFs are known, reliability can be identified for a given number of cycles. As we are focusing on the lifetime of the product, we need to determine the moment (number of cycles) when the reliability of the part reaches the security limit. Thus, we have to consider the Wöhler design variable as a probabilistic model of the material elasticity limit versus lifetime. This information is derived (see Figure 3a) from the known distribution of cycles to failure at two stress levels [5]. Then, we repeat the reliability estimation for several different numbers of cycles which lead to the time dependant reliability evolution.
RESULTS
 |
|---|
Our method provides a way of assessing and comparing two wheelchair designs, especially their frames. In this application, only the wheelchair structures differ.
If we assume a security level for the reliability under which the user security is not guaranteed anymore, we can determine the lifetime of the wheelchair. As shown in Figure 3b, the wheelchair with the higher number of cycles before falling under the security limit is the best design for the chosen scenario, i.e. the one presenting the longest lifetime.
CONCLUSION
Our method proposes a way to compare wheelchair designs from a lifetime point of view, by using our time dependent upgraded approach. The availability of these results at the design stage, with few data and calculation requirements, allows repeated reliability assessments for a whole period of use. Thus, the product lifetime evaluation can be achieved.
The lifetime prediction for a wheelchair will help designers to improve the most solicited parts of their product. Their collaboration with occupational therapists will help them to focus on several failure modes for specific parts: for instance, the impact of spasms on the frame, the headrest and the footrests, etc. We plan to apply this research to existing wheelchairs, in collaboration with manufacturers.
REFERENCES
- ISO 7176-8, “Exigences et methods d'essai pour la résistance statique, la résistance au chocs et la résistance à la fatigue” (1998).
- Haldar A, Mahadevan S, “Probability, Reliability and Statistical Methods in Engineering Design” New York: John Wiley & Sons (2000).
- Zwingmann X, Aït-Kadi D, Coulibaly A, Mutel B, “Estimation de la fiabilité des produits manufacturés au stade de leur conception” Québec: 5th Int. Industrial Engineering Conference (2003).
- Lewis EE, “Introduction to Reliability Engineering” New York: John Wiley & Sons (1987).
- Murty ASR, Gupta UC, Radha Krishna A, “A new approach to fatigue strength distribution for fatigue reliability evaluation” Int. J. Fatigue 17(2): 85-89 (1995).
ACKNOWLEDGMENTS
This project is supported by the Natural sciences and engineering research council of Canada (NSERC) and by the International Council for Canadian Studies (ICCS). Authors address special thanks to Mr. François Routhier, Eng.,M.Sc, Ph.D. student at CIRRIS, for his suggestions and comments.
Author Contact Information:
Xavier Zwingmann,
Laval University,
Mechanical Department (Pav. Pouliot),
Québec, Qc G1K 7P4,
Office Phone (418) 656-2131 # 16747
Email: xavier.zwingmann@centor.ulaval.ca
