RESNA Annual Conference - 2010

BACKGROUND

Recognition of UE arthropathy and degenerative arthritis associated with longer-term assistive device use has been reported in current literature [1, 2]. Individuals with weaker lower extremities frequently rely on assistive devices such as walkers, canes and Lofstrand crutches for ambulation. Among these, walkers provide the most support but restrict activities of daily living (ADLs). Canes provide the least support and most freedom to perform ADLs. Lofstrand crutches strike a balance between support and freedom required to perform ADLs.

A few previous studies have quantified UE dynamics during Lofstrand crutch-assisted gait. Among those, Slavens et al. investigated a pediatric population and established a standardized UE inverse dynamics model [3]. However, the cuff forces and moments where considered negligible [3]. Also, the placement of the sensor at the tip of the crutch increased the moment of inertia during crutch swing. Requejo et al. presented a system with a lower moment of inertia by locating the sensor proximal to the handle of the crutch [4]. However, this system evaluated only the cuff moments from which the cuff forces were derived [4]. This crutch model was applied to a single adult SCI subject. Liggins et al. used a crutch system similar to Slavens et al. but did not fully quantify the UE dynamics [5].

The goal of this study was to develop a pediatric Lofstrand crutch model, which provides a complete quantitative description of the UE dynamics during crutch-assisted gait. This model is standardized based on ISB recommendations [6] and includes both cuff forces and moments. The system is versatile for application with various pathologies. The system can evaluate repetitive loading during ambulation and may prove helpful to develop gait strategies for safer, longer-term crutch usage.

RESEARCH QUESTION

The objective of this study is to develop a system capable of characterizing UE joint dynamics in children using Lofstrand crutches. The goal is to identify UE joint loading patterns associated with various pathologies. Studies have shown that Lofstrand crutches require loading of the UEs up to 50% of body weight, without including the involvement of the cuff forces and moments [7]. Evaluation of the UE kinetics in a pediatric population of OI, SCI and CP is used in this study to gain further insight into the demands placed on the UEs. We hypothesize that these populations will exhibit similar joint load demands.

METHODS

Kinematic Model

The UEs were modeled using seven rigid body segments, which were the thorax, upper arms, forearms, and hands. Each crutch was modeled using three rigid body segments defined by the cuff, handle and tip of the crutch. Thirty-two reflective markers were used to define these segments.

Joint centers were calculated using the markers and subject specific anthropometric data. Joint coordinate system axes were based on ISB standard recommendations [6]. The thorax model was based on the study done by Nyugen et al. for analyzing thorax kinematics in children with myelomeningocele (MM) [8].  A Z-X-Y Euler rotation sequence was used to define rotations of the segments.

Kinetic Model

The kinetic model was developed using the inverse dynamics Newton-Euler approach [9]. The reaction forces and moments from the instrumented crutches are required for solution of the model. The Newton-Euler equations were used for each joint to compute the forces and moments.

Instrumentation

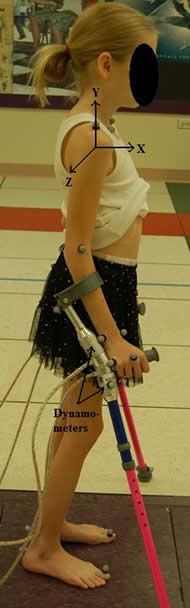
Crutches were instrumented with six-axis FS-6 dynamometers (AMTI, Watertown, MA) to measure the applied reaction forces and moments. Each crutch consists of two dynamometers placed above and below the handle (Photo 1). Thin co-axial cables are used to multiplex crutch data for acquisition. The analog data from the dynamometers are amplified using AMTI MSA-6 high gain amplifiers. The weight of the dynamometers was 0.10 kg each and the weight of the crutch was 0.43 kg. All force and moment data were validated and calibrated with static and dynamic validation protocols.

Patient Population

One subject from each of the three different populations with prior experience using Lofstrand crutches was selected. A subject with type I OI, 16-year-old female participated. Her height and weight were 1.4 m and 43.8 kg respectively. The subject with SCI was a 7-year-old female of height 1.2 m and weight 20.4 kg. The subject with CP was an 11-year-old female and her height and weight were 1.4 m and 24.9 kg respectively

Data Collection, Processing and Analysis

The subjects were asked to walk with the bilateral instrumented Lofstrand crutches on a 6-meter walkway for 3 trials at a self-selected pace and gait pattern. A Vicon motion analysis system, with 14 infrared cameras, was used to capture 3D motion of the reflective markers placed on the bony landmarks of the subject and the crutches. Data were averaged over 3 trials. Foot heel strike to heel strike was defined as 100 % gait cycle with data being processed every 1 % of the gait cycle.

Cadence, walking speed, stride length and stance duration were calculated for each subject. Forces and moments were determined. Mean forces and moments were normalized to % body weight (BW) and % body weight multiplied by height (% BW*H).

RESULTS

All UE joint data was collected and analyzed. The shoulder consistently showed the highest joint reaction forces and moments and is reported here. Temporal distance parameters of the three subjects are reported (Table 1.). It was seen that all subjects adapted a similar two-point gait pattern. The OI subject demonstrated maximum cadence, walking speed and a high stride length. This subject had the lowest range of motion, peak forces and moments at the shoulder. The SCI subject had the lowest walking speed and stride length, with the highest stance duration. The range of motion and the forces at the shoulder were highest in this subject. The subject with CP demonstrated lowest cadence and stance duration while the highest stride length. Highest peak moments at the shoulder were observed in this subject.

The sagittal plane joint reaction forces and moments occurring at the shoulder are demonstrated in Fig 1. Highest force was seen in the subject with SCI. Superiorly directed compression shoulder forces were sustained for up to 50% of the gait cycle while peaking at 31.33 % BW. The shoulder forces for the subjects with OI and CP have similar patterns where superior compression forces were sustained for up to 45% of the gait cycle. Moments are similarly varied among the three pathologies. The maximum shoulder flexion moment was seen in the subject with CP.

DISCUSSION

Table 1:Temporal Parameters, Shoulder Kinematics and Kinetics

Subject	Cadence (Steps / min)	Walking speed (m/s)	Stride Length (m)	Stance Duration (%)	Range of Motion (degrees)	Peak Forces (%BW)	Peak Moments (%BW*H)
OI	103.39	0.78	0.90	65.57	25.15	9.14	2.05
SCI	93.99	0.49	0.62	70.76	34.23	14.96	3.78
CP	78.59	0.62	0.95	56.14	42.63	31.33	2.11

Our data indicates that the subject with OI was the least dependent crutch user since she had the least superiorly acting compression forces and flexion moments at the shoulder. This is consistent with an effort to reduce overall skeletal loads to minimize fractures. On the other hand, the subject with SCI was the most dependent crutch user, which is consistent with the slower walking speed and higher forces occurring at the shoulder. The subject with CP moderately loaded her UEs during crutch ambulation, but demonstrated high flexion moments during the gait cycle. Even though all the subjects showed similar two-point gait patterns, the force and moment loading varied. It may be significant that several joint load patterns exhibited forces exceeding those of typical wheelchair users [10].

Results of this study support the use of this technically validated crutch system to evaluate UE ambulation patterns during Lofstrand crutch-assisted gait. Limitations of the previous studies have included limited number of sensors, sensor location, sensor characteristics and a non-standardized model. These limitations were addressed by designing a novel crutch system that included more sensors placed strategically for complete analysis of the UE dynamics.

Earlier work by our group indicates that crutch-assisted gait patterns directly affect UE joint load distribution [3]. The current kinetic model will allow study of joint load optimization through activity modification, gait training and crutch re-design. Further study with this system may also offer valuable insight for crutch prescription, placement patterns (reciprocal, swing-through, swing-to) and longer-term usage effects.