INTRODUCTION

Gait disorders and falls rank amongst the most frequent functional disorders of elderly patients. While the ability to locomote feels natural to healthy people, walking challenges many persons with advanced age. Changes triggered by the physiological ageing process, like declining muscular strength, degenerating visual perception, and decreasing nerve conduction velocity, but also illness-related issues e.g. of the muscular-skeletal system, lead to a more or less typical change of the human gait pattern and increase the risk of fall. Consequently, gait disorders and falls represent significant challenges in geriatric diagnostics and therapy.

The project ModESt, funded by the German Federal Ministry of Education and Research in context of the KMU-innovativ program (2017-2019), is dedicated to reduce the risk of fall for elderly people using wheeled walkers. Our approach is to monitor gait properties with walker-mounted sensorial equipment, and give valuable feedback to the user about insecure gait properties to be corrected. A long-term goal of the project is to provide a diagnostic tool for physicians and physio therapists with which the assessment of current procedures, such as the Timed up and go Test, can be objectified. In this context, the publication at hand addresses the research question of whether a robust classification of clinically significant gait properties, e.g. stride-variability and -length, is possible by solely evaluating a small number of distance measurements sensed by an instrumented walker. In the following we do so by stating related works, presenting the technical methods used, and informing about an observational clinical study that evaluates the approach presented.

Related Work

Today's gait analysis systems assess time-series of measurements, and can be differentiated w.r.t. a broad range of sensorial equipment applied. Common approaches use retroreflective markers in combination with multi-camera setups to track tagged joints and limbs in 3D [1-3], measure dynamic electromyography patterns of activated muscles during gait [4,5], monitor joint angles and acceleration data by body-mounted inertial measurement units [6,7], or analyze foot pressure by the help of sensor pads within shoes or on the ground. These approaches require extensive preparation of the test person or the environment, rendering test sessions outside the laboratory almost impossible. With these necessities in mind, the instrumentation of walking aides such as wheeled walkers is appealing. It does not only render the location-independent monitoring of a person's gait possible, but it also allows for the observation of risk of fall factors during the daily use of wheeled walkers.

Ballesteros et al. have presented the walker platform i-Walker [8]. The system is equipped with pressure-sensitive handlebars and odometry-enabled back-wheels. Using this setup, the authors correlate measurable parameters such as step-time and -length as well as stride-time and -length to the Tinetti clinical scale [9].

METHODS

Data Representation and Acquisition

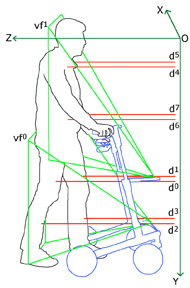
Let a vector of $n$ distance measurements taken at time $t$ be defined by $D_t:=\left[d_t^0,...,d_t^{n-1}\right]:n\in \mathbb{N},t\in \mathbb{R},d_t^i\in \mathbb{R}$ . Then we can define a time series of $n\times m$  distance measurements starting at $t_0$  and ending at $t_{m-1}$  by the matrix $D_T:=\left[D_{t_0},...,D_{t_{m-1}}\right]:t_i\in T\subset \mathbb{R},t_i{t}_{i+1}$ . $D_T$  can not only represent the complete set of measurements taken during data acquisition, but also time-continuous subsets. In particular, we are interested in measurement intervals that compose a single gait cycle, since this is the atomic unit that we want to classify. In the long term, it is planned to capture $D_T$  by several small-scale and low-cost infrared proximity sensors. To be more flexible during the development phase, we currently use two Asus Xtion Pro depth cameras, mounted at the walker’s front (cf. Figure 1 ), for sensing the distance to the user's body. We sample from the depth camera's data so-called virtual distance sensors (VDS), i.e. we intersect single measurement rays with the raw depth images. Note that the depth measurements of both cameras are transformed into a common frame of reference before the sampling step (cf. [10]). This allows us to define the pose of the VDS in dependence of the person's body height.

Gait Cycle Extraction and Filtering

The human gait cycle is defined by the period of time in-between the starting points of two consecutive ground contacts of the same foot. Since a single measurement $D_T$  doesn't provide us any direct information about whether or not a foot touches the ground, we get by with partitioning the periodic movement pattern at points in time where one of the distance measurements $d^i$ , that intersects with the leg closest to the ground, is maximal (e.g. $d^2$  in Figure 1 ).

Having split the stream $D_T$  at two consecutive minima of $d^2$ , e.g. at $t=j$  and $t=k$ , we can extract a new gait cycle candidate $D_{T\text{'}}$ , with $T\text{'}=\{j,...,k\}\subset \mathbb{R}$  for subsequent processing. As not every single gait cycle is suited for being fed into the classification knowledge base, or being matched against it, we continue by filtering out gait cycle candidates that show data from unusual walking behavior, such as turning on the spot or backwards movements. We do so as follows: let

$$\mathrm{GC}{C}_T:=\left[D_{T_i}\right]:T_i\subset T\subset \mathbb{R},T_i\cap T_{i+1}=\phi$$ (1)

be the vector of potential gait cycle candidates extracted from recently recorded distance measurements. Then we can filter out gait cycle candidates that are too long or short over time, compared to the average duration of gait cycle candidates. In addition, we remove gait cycle candidates that show value ranges of $d^i$  differing too much from the average value range of $d^i$  over all gait cycle candidates. This yields the following definition of detected gait cycles:

$G{C}_T:=\left[D_{T_i}\right]:D_{T_i}\in \mathrm{GC}{C}_T,1-{ϵ}_1<\frac{\left|T_i\right|}{\phi {\Delta }_t\left(\mathrm{GCC}\right)}<1+{ϵ}_1,1-{ϵ}_2<\frac{v{r}_j\left(D_{T_i}\right)}{\phi v{r}_j\left(\mathrm{GCC}\right)}<1+{ϵ}_2$                                                         (2)

In (2), $\left|T_i\right|$  denotes the duration of $D_{T_i}$ , $\phi {\Delta }_t\left(\mathrm{GCC}\right)$  denotes the average gait cycle duration over all gait cycle candidates in GCC, $v{r}_j\left(D_{T_i}\right)$  denotes the value range of the $j_{\mathrm{th}}$  distance measurement of $D_{T_i}$, and $\phi {\Delta }_t\left(\mathrm{GCC}\right)$ denotes the average value range of the $j_{\mathrm{th}}$  distance measurement over all gait cycle candidates in GCC. For the current implementation, we chose ${ϵ}_1=0.25$  for limiting the duration deviation of gait cycles, and ${ϵ}_2=0.5$  for filtering out gait cycle candidates with deviating value range.

Classification of Gait Cycle Descriptions

As gait cycles can vary in their duration, all gait cycles in  are initially resampled, i.e. linearly interpolated over time. In our current implementation, we compute 30 interpolated distance values per gait cycle for each VDS. In the following we indicate the normalized length of time of gait cycles by replacing the subscript T by $T^{\prime }$ , e.g. we write $G{C}_{T^{\prime }}$  for a set of gait cycles with normalized length over time.

The core task of the system presented in this paper is now to classify a single gait cycle description $D_{T^{\prime }}$  w.r.t. a discrete-valued gait cycle property P. Let for example $P_{\mathrm{sh}}(D_{T^{\prime }})\in \left\{\mathrm{normal},\mathrm{reduced}\right\}$  be the stride height of a person's gait cycle that can be assessed by a physiotherapist as being normal or reduced. During the training phase of the classification algorithm, gait cycles out of the training dataset are clustered according to their ground truth labels. A cluster's centroid, along with the covariance matrix over the corresponding training samples, finally makes up an entry into the knowledge database. For our stride height example, let $$G{C}_{T^{\prime }}^{\mathrm{tr}}\left(\mathrm{sh}.\mathrm{norm}\right)$$ now be the training data that describe gait cycles with a normal stride height. Please recall that normalized gait cycles are composed of $n$  VDS, and $m$  readings over time per VDS. We can then formulate the covariance matrix as

$C(\mathrm{sh}.\mathrm{norm})=\left(\begin{array}{cc}c(X_1,X_1)& c\left(X_1,X_{\mathrm{nm}}\right)\\ c\left(X_{\mathrm{nm}},X_1\right)& c\left(X_{\mathrm{nm}},X_{\mathrm{nm}}\right)\end{array}\right),c(X_i,X_j)=\frac{\left(x_i-{\mu }_i\right)\left(x_j-{\mu }_j\right)}{\left|G{C}_{T^{\prime }}^{\mathrm{tr}}\left(\mathrm{sh}.\mathrm{norm}\right)\right|}$                                                        (3)

with $X_{\mathrm{im}+j}$  being the $j_{\mathrm{th}}$  reading of the $i_{\mathrm{th}}$  VDS, interpreted as random variable over all gait cycles in $G{C}_{T^{\prime }}^{\mathrm{tr}}(\mathrm{sh}.\mathrm{norm}),c\left(X_i,X_j\right)$  being the single (co)variance terms, and $\left|G{C}_{T^{\prime }}^{\mathrm{tr}}(\mathrm{sh}.\mathrm{norm})\right|$  being the number of gait cycles with normal stride height in the training data set. After having computed the centroids and covariance matrices of all classes p for a given gait cycle property P, we compute the most similar class of a given gait cycle description to test. We do so by minimizing the Mahalanobis distance d [11] over all $p\in P$  as follows:

$\arg {\min }_{p}d\left(D_{T^{\prime }}^p,D_{T^{\prime }}\right)=\arg {\min }_p\sqrt{{\left(D_{T^{\prime }}^p\right)}^T{C}^{-1}\left(D_{T^{\prime }}^p-D_{T^{\prime }}\right)}$                                                                                              (4)

In (4), $D_{T^{\prime }}^p$  describes the centroid of a given class p for a given gait property, $D_{T^{\prime }}$  describes the gait cycle description to be tested, and $C^{-1}$  describes the inverted covariance matrix belonging to $D_{T^{\prime }}^p$ . For all vector- and matrix-related operations, including the computation of the inverse of C, we use the C++ template library Eigen.

Study Design and Procedures

The main experimental evaluation of the proposed classification algorithm took place at the Bremen Nord Hospital - Clinic for Geriatrics and early Rehabilitation. Here, 26 stationaries and out patients aging from 47 to 93 years (Ø74.3) underwent an observational clinical study that had been approved by the responsible ethical panel beforehand. The study design included initial clarification for the patients about the goal of the study, followed by the patients' signature under a consent that allowed us for the usage of the anonymized data collected. In the following, the undisclosed part of a case report form was filled out by a physician for every patient. These anonymized documents do not allow somebody to draw conclusions about the identity of the patients under scope. Beside personal information, this part included medical diagnoses, i.e. the reasons for the patients’ hospital stay was not transmitted to the study team.

In the following, each patient was asked to walk up and down an approx. 12m long hallway in the physiotherapeutic department for three times, while being supported by the instrumented walker. In between each trial the subjects had sufficient time for relaxation. During the three trials, physiotherapists and a physician observed the gait properties of the subject and noted their observations afterwards in the second part of the case report form. This open document includes a unique identifier for each patient that connects to the undisclosed part of the case report form. Table 1 lists all 14 gait properties and their value ranges, as assessed by the medical staff. In parallel to the visual examination of the patients, two Asus Xtion Pro depth cameras, mounted at the walker and connected to a Raspberry 3, recorded depth information of each trial.

After the data acquisition sessions, depth information log files were separated into training data and test data log files, i.e. we used the log files of the first two trials of each participant as the training data set, and the third one as the test data set. Gait cycles were then extracted and filtered for each log file. According to the case report forms, gait cycles from the training data sets that described the same class of a gait cycle property were then bundled and used to compute the mean gait cycle description (centroid) and inverted covariance matrix for that class. In the following test phase, we computed the Mahalanobis distance to the classes of each gait cycle property for each filtered gait cycle from the participants’ third trial-log file.

ANALYSIS AND DISCUSSION

Table 1 . Ground truth distribution observed by clinical staff during training of the classification algorithm

Gait Property	Class 1		Class 2		Class 3		Class 4		Class 5
2 gait pattern (2gp)	physiological	28.6%	pathological	71.4%	―		―		―
5 gait pattern (5gp)	physiological	28.6%	antalgic	20.4%	protective	30.6%	atactic	8.2%	paretic	12.2%
position to walker (ptw)	centered	51.0%	left deviating	40.8%	right dev.	8.2%	―		―
distance to walker (dtw)	normal	57.1%	increased	42.9%	―		―		―
hip flection left (hfl)	0°-10°	59.2%	10°-30°	38.8%	>30°	2.0%	―		―
hip flection right (hfr)	0°-10°	44.9%	10°-30°	44.9%	>30°	10.2%	―		―
Knee flection left (kfl)	<0°	12.8%	0°-10°	72.3%	10°-30°	10.6%	>30°	4.3%	―
knee flection right (kfr)	<0°	12.8%	0°-10°	63.8%	10°-30°	23.4%	―		―
torso flection (tf)	upright	36.7%	anteflexed	59.2%	retroflexed	4.1%	―		―
stride symmetry (ss)	uniform	46.9%	left deviating	24.5%	right dev.	28.6%	―		―
stride width (sw)	normal	69.4%	narrow	16.3%	broad	14.3%	―		―
stride variability (sv)	regular	61.2%	slightly incr.	20.4%	irregular	18.4%	―		―
stride length (sl)	normal	61.2%	reduced	34.7%	increased	4.1%	―		―
stride height (sh)	normal	65.3%	reduced	34.7%	―		―		―

By comparing the most similar class of a tested gait cycle description with the ground truth taken from the case report forms, we acquired the basic data for setting up the statistics over correct and false classifications. Statistics such as the minimal, maximal, and mean classification rates, as well as the standard deviation of classification rates (for a given gait cycle property) are given in Figure 2. In addition to the classification rates of single gait properties, we have compared the cadence rates (number of gait cycles per minute) for each participant, i.e. as measured by hand during data acquisition (ground-truth) vs. one minute divided by the mean length of time of extracted and filtered gait cycles of subjects as computed by the system.

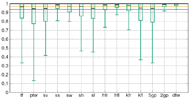
Results show best classification rates (cr) for two-valued gait properties such as distance to walker (99.4%), and the meta-property 2 gait pattern (99.2%), which discriminates between physiological and pathological gait. With 94.2%, position to walker shows the worst cr. The average cr over all gait properties is given by 96.9%. The mean cadence rate measurement error is given by 1.86% (: 7.06%, max error: 18.2%) over all subjects.

CONCLUSIONS

This paper presented an add-on system for wheeled walkers that allows for the online classification of the user’s gait cycles w.r.t. 14 gait properties relevant in assessing gait safety. Now that an initial observational study has proven robust classification rates, ongoing and future work develops in three directions. On the first hand we are developing a suitable user interface that communicates problematic postures and gait properties to the user. In parallel, the depth cameras used here are replaced by small-sized Time-of-Flight laser-ranging sensors allowing for a seamless integration into the walker frame. With the final walker setup available, we will conduct an interventional study that is dedicated to the question of whether recognized and communicated gait problems can improve patients’ gait in sense of correct and safe gait.