INTRODUCTION

Wheelchair seat cushions are designed not only to provide comfort, but also to aid in stability, body positioning, effective transfer performance and pressure distribution. While an appropriate wheelchair seat cushion provides the user with more function in their wheelchairs, using an unsuitable cushion can be catastrophic. [1,2] Therefore, recommending the right cushion based on user needs is of utmost importance in the field of wheeled mobility. When prescribing a wheelchair cushion, a clinician makes their decision based on certain factors such as the user’s anatomical needs, previous trials and experience. Although there are benefits to having a large variety of cushions to choose from, it can be difficult to translate each of these cushion’s individual properties into clinical necessity. To do so requires objective information regarding the performance of the cushions, which can be transcribed into what would be best practice for the wheelchair user. [3]

ISO 16840-2, Determination of physical and mechanical characteristics of seat cushions intended to manage tissue integrity, is a published standard by the International Organization of Standardization that provides test methods used to characterize cushion performance. The standard has been adopted and improved as RESNA WC-3, Section 2. Although the rationales link the measured quantities to clinical relevance for the end user’s experience, the standard also states that “the link to clinical efficacy, although implied, has not been validated.” [4,5]

Two specific test methods described in WC-3 Section 2, impact damping and hysteresis, are both tests used to characterize cushions’ dynamic behavior. The impact damping test denotes a cushion’s ability to dissipate energy to reduce the impact of loading on the tissues and maintain postural stability. [4] In real case scenarios, loading impacts must be dealt with when a wheelchair goes over obstacles or rolls off a curb. This is an important performance characteristic since tissues are made more susceptible to pressure injury when they are exposed to higher magnitude of loading or multiple impacts. On the other hand, the hysteresis test measures the amount of energy that is lost to the wheelchair cushion during a cycle of compression and unloading. When a wheelchair is going down a flight of steps or traversing rough terrain, a cushion with a larger hysteresis transfers less energy onto the user’s tissues and consequently absorbs more energy. [4]

Standards claim that there is a relationship between impact damping and hysteresis. While the possible link between the two has been explored in the past by Hillman et al., [3] the ISO standard has since been revised. The previously published version of the standard (2007) evaluated impact damping using rebound parameters. Chung and Sprigle promoted analysis of impacts instead of rebounds, since largest tissue compression occurs at impact accelerations, and consequently better represents clinical conditions. [6,7] Further, the ISO 2007 standard did not control for placement of the accelerometer. This introduced variability in test results since the acceleration is a function of distance to the axis of rotation. [7] This issue has been addressed in the revised ISO 2018 standard. Change in recovery time is also an important aspect of the standard that has been revised. In the former standard, the hysteresis test was conducted as step-wise loading at 2-minute intervals. The newer version has eliminated the recovery time and is a continuous compression-unloading cycle.

The objective of this study was to first establish the intralaboratory repeatability of the 2018 standard impact damping and hysteresis tests and indicate their ability to differentiate between cushions. Following this, the aim was to examine if a relationship exists between the two tests as per the rationale provided in the standards.

MATERIALS AND METHODS

A cohort of 21 cushions were selected on the basis of healthcare codes by the Centers for Medicare and Medicaid Services (CMS) and material of construction that collectively provides a good representation of what is commercially available to wheelchair cushion users. Previous literature was analyzed to ensure that the selected cushion cohort contained cushions previously tested as well as untested cushions.  

Prior to testing, all cushions were preconditioned and acclimated to the test environment as per the standard. To minimize errors in positioning, a line called the “IT line” was marked on each cushion to dictate the placement of the ischial tuberosities, or base points of the indenters on the cushion. The impact damping test uses a Rigid Cushion Loading Indenter (RCLI). The RCLI is designed to resemble the anatomical dimensions of a 50% percentile male human buttock and thighs with a weight totaling 500N ± 10N. A 3-axis GP1 Programmable Accelerometer (Sensr, USA) at 10g was affixed on top of the RCLI such that one axis is oriented to measure normal to the top surface. The accelerometer includes an analog 2 pole Butterworth low pass filter at a cut-off frequency of 45Hz. A hinged rigid plate with two rubber stops is used to support the cushion and indenter at an angle of 10 ± 1 degrees. An alignment board capable of sliding antero-posteriorly was positioned at the anterior edge of the indenter. A laser pointer fastened to the top of the frame directs consistent placement of the accelerometer from the hinged edge of the plate (axis of rotation). To conduct the test, the cushion and RCLI were positioned on the rigid plate and a support is pulled such that the rigid plate rotates down onto its rubber stops (from 10 degrees to horizontal). This test was repeated for a total of three trials per cushion. The metrics calculated were the magnitude of the first impact (I1), magnitude of the second impact (I2), ratio of the second impact to the first (I2:I1) and the ratio reported as a percentage.

The hysteresis test used an RCLI attached to a loading rig (Alliance RF 100, MTS Corporation). The loading rig with RCLI applied a preload of 8N to the cushion, and then cycled from 8N to 750N and back at a rate of 1 mm/sec. The thickness of the cushion under the basepoints of the RCLI was calculated at different forces during compression and unloading. The test was repeated for a total of three trials per cushion. Hysteresis indices were calculated for 250N by subtracting the quantity of the average unloading thickness at 250N divided by the average compressive thickness a 250N from 1. Hysteresis indices were calculated for 500N using the same calculation but with values obtained at 500N. 

The data from the accelerometer was analyzed using a MATLAB script. An intraclass correlation coefficient (ICC) and repeatability coefficient (RC) was processed for all the measured parameters. Two values from the intraclass correlation were obtained, the single rater ICC and the average rater ICC. The ICC and RC assess the repeatability of a test protocol, and its ability to distinguish between cushions. The ICC was computed using a two-way mixed effects model under the Absolute agreement definition. The RC value shows the test-retest reliability and is calculated as the standard deviation between trial measurements multiplied by 1.96 and √2. [8,9]

RESULTS

Table 1. ICC and RC for impact damping and hysteresis test parameters

	h250	h500	I1	I2	I2:I1
Single ICC	0.985	0.944	0.922	0.951	0.977
Average ICC	0.995	0.981	0.973	0.983	0.922
RC	-	-	0.351 g	0.215 g	3.920%
Mean ± SD [Range]	0.153 ± 0.086 [0.030 - 0.433]	0.112 ± 0.056 [0.027 - 0.238]	2.777 g ± 0.432 g [2.067 g - 3.560 g]	1.125 g ± 0.343 g [0.650 g - 1.858 g]	38.852 % ± 9.030 % [22.449 % - 57.351 %]

Table 1 shows the ICC and RC for the impact damping metrics and hysteresis indices. The RC values for hysteresis could not be calculated due to a trend in results of the three trials.

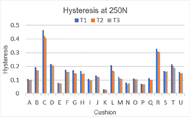
Figures 2-3 show hysteresis indices and impact damping ratios. To quantify the relationship between the impact damping and hysteresis tests, a Pearson’s correlation was applied between the metrics of both tests. The results of the correlation are given in Table 2.

 

DISCUSSION

On observing the data in Table 1, it can be noticed that the values of ICC are quite high for both single ICC and average ICC across every metric, indicating that the test protocol is highly reliable for a single or multiple replications. [9] The large range of values across each parameter combined with the high ICC values shows that the tests can distinguish between cushions.

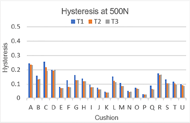
The hysteresis values obtained from this study ranged from 0.030 to 0.433 for h250 and 0.027 to 0.238 for h500. These are quite similar to the ranges of 0.041 to 0.307 for h250 and 0.023 to 0.223 for h500 obtained by Hillman et al. [3] Figures 2 a and 2 b depict the cushion hysteresis indices at 250N and 500N for the three trials. Close examination of the graphs shows that in majority of the cases, the first trial shows a larger hysteresis than the subsequent two trials. This could be attributed to two reasons, namely, not giving the cushion enough time to recover post trial, or not appropriately resetting the cushion. The protocol followed allowed each cushion to rest for approximately 5 minutes between trials. Given that the standard calls for a minimum recovery time of 5 minutes, a longer time should have been allotted to each cushion to regain its full thickness. Since certain cushions contain materials that get displaced while testing, proper care should be ensured to reset it according to manufacturer instructions. Bafana had observed a similar trend and concluded that the RC calculated for hysteresis is not reported because it would not be a true representation of the test’s repeatability. However, this does not show a low repeatability, it just indicates that the readings are systematically different and so the RC does not consider them to be true replicates. [10] The RC values computed for the impact damping test show that the repeatability between trials is better for the second impact than the first, however the values are quite small, so the test-retest repeatability and precision of the test are very good. Additional work is needed to assess interlaboratory repeatability as well as repeatability when the cushions are tested again in this laboratory.

Table 2. Pearson’s correlation between Impact Damping and Hysteresis test parameters

Correlations	Correlation Coefficient (n=21)	Significance
I1 with h250	0.164	p=0.479
I1 with h500	0.015	p=0.948
I2 with h250	0.001	p=0.997
I2 with h500	-0.101	p=0.662
I2:I1 with h250	-0.128	p=0.581
I2:I1 with h500	-0.242	p=0.290

The Pearson’s correlation coefficients observed in Table 2 shows that the relationship between impact damping and hysteresis is quite weak, with no statistical significance in any of the correlations. It was hypothesized that the most representative characteristics of the impact damping test would be the ratio of the two impacts and the magnitude of the first impact. A cushion having a lower I2:I1 ratio shows that more energy was absorbed by the cushion during impact and hence the magnitude of the second impact was greatly reduced. Since hysteresis is described as a loss of energy in a cycle of loading and unloading, a cushion with a low impact ratio should have high hysteresis indices. This is in line with the negative correlations seen between the impact ratio and the two hysteresis measures. Theoretically, this relationship can be further expanded to say that a higher first impact magnitude should correlate to higher hysteresis indices; however, this cannot be practically applied. According to Annex B of the standard, a greater first impact could indicate a stiffer cushion. [4] Nonetheless, a stiffer cushion also allows a lower deformation under a compressive load which leads to a lower hysteresis. [11] However, there was a weak correlation between the first impact and hysteresis indices. The correlation between the second impact and hysteresis at 250N are shown to be almost independent of each other, and the correlation between the second impact and hysteresis at 500N have a very weak negative correlation.

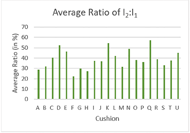
The data from this study show that the correlations between the two tests’ metrics are quite weak. Although the discrepancy in recovery time has been reduced, the loading time scales between the two tests are still different. The time of recovery in the impact damping test is dependent on the time between consecutive impacts, while the time of recovery in the hysteresis test is dependent on the speed at which the loading and unloading occurs. The study conducted by Hillman et al. used both rebounds and impacts to examine the relationship between the two tests on a set of 37 cushions. [3] Comparing this study with Hillman et al. revealed that the correlations were similar except in the case of the correlation of I1 with h250, where they found a weak negative coefficient. However, the coefficients are also very close to zero, indicating the first impact is independent from hysteresis. It is also interesting to note that they found the correlations between the rebounds and hysteresis were stronger than those for impacts. Additionally, when a subset of cushions was selected to represent a simpler construction, the correlations of the rebound ratio with hysteresis was quite high with statistical significance achieved.

Despite the fact that the test results have not shown a significant association as indicated in the standard’s rationale, it is still important to note that the change in recovery time and consideration of impacts as opposed to rebounds has not changed the weak relationships between the two tests’ metrics. It should also be noted that given the complex nature of some of the cushions, it would be useful to sub categorize the cushions to represent samples that are more similar to each other to reduce the variability that comes with different material constructs. Doing so can provide a clearer picture of the perceived link between impact damping and hysteresis, and once established, can be applied to a more varied sample.